Prírodou inšpirované algoritmy

Parametrické

Pri reprezentácii niektorých štruktúr je do tejto chvíle zavedený súbor symbolov (príkazov pre korytnačku) nepostačujúci. Napríklad úsečky rôznych dĺžok a natočenie o rôzne uhly sme realizovali opakovaním príslušných symbolov. Bolo to nejako neprehľadné a naviac použiteľné len pre prípad celočíselných násobkov. Čiastočným riešením druhého problému je zavedenie špeciálnych symbolov pre zmenu aktuálneho uhla α, resp. jednotkovej dĺžky posunu o nejaký menší prírastok, ale ďalej to zhoršuje prehľadnosť zápisu. Pre vyriešenie naznačených problémov boli navrhnuté parametrické L-systémy (Lindenmayer,1974). Jednoduchšia verzia týchto systémov umožňuje symboly pre pohyb a natočenie korytnačky doplniť o číselný parameter, udávajúci hodnotu posunu, resp. natočenia. Okrem toho sú doplnené nové symboly s číselným parametrom, napríklad pre zmenu hrúbky a farby čiary.

Omnoho širšie možnosti ponúka použitie symbolických parametrov a doplnenie pravidiel o podmienkovú časť, tvorenú logickým výrazom, obsahujúcim formálny parameter. Jednému nahradzovanému symbolu potom odpovedá viac pravidiel s disjunktnými podmienkovými časťami. Výber pravidla je daný splnením jeho podmienkovej časti po dosadení skutočnej hodnoty parametra nahradzovaného symbolu.

Naznačený mechanizmus umožňuje navrhnúť modely, v ktorých sa mení charakter vývoja rastliny s postupnou zmenou nejakého parametra. Napríklad nasledujúci systém (dvojbodka oddeľuje bežnú ľavú stranu pravidla od podmienkovej časti) :

Axiom = A(0)
α = 30°
A(p) : p < P → F[+L][-L]A(p+d)
A(p) : p = P → F[+L][-L]B
B → K

generuje rastlinu s priamou stonkou, postupnosťou dvojíc listov L proti sebe a vo chvíli, keď rastúci parameter p dosiahne medznú hodnotu P, objaví sa na konci stonky kvet K. Na nasledujúcich obrázkoch sú znázornené tretia, štvrtá a piata itarácia ( P = 2 ).

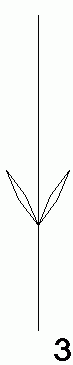
O vkladaní objektov (listu, kvetu, apod.) pojednáme neskôr. Parameter p môže reprezentovať hromadenie nejakej látky, ktorá po dosiahnutí istej úrovne stimuluje rast kvetu, alebo môže tiež reprezentovať diskrétny nárast času potrebného pre vytvorenie kvetu (obidva mechanizmy boli u prírodných rastlín pozorované).