Prírodou inšpirované algoritmy

Simulácia

Pred začatím simulácie program ponúka množstvo nastavení druhu simulácie a jej výstupu (viď dialóg na nasledujúcom obrázku). K týmto sa však vrátime neskôr a teraz prejdeme k simulácii priamo - prijatím prednastavených hodnôt nastavení (príkaz d)

Objaví sa Vám dialóg, ktorý je znázornený na obrázku dole, opäť zadajte d.

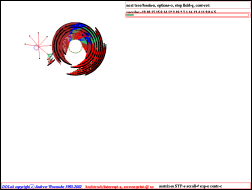
Program začne vykresľovať graf stavových prechodov pre všetky stavy siete. Tento proces može trvať pre veľký stavový priestor (v tejto simulácii 220 stavov) na pomalších počítačoch dosť dlho. Na procesore AMD 300Mhz trvala simulácia 47 minút, na Pentiu III 866MHz zhruba štyri minúty, a na procesore AMD Athlon-XP 2500+ to bolo čosi vyše 47 sekúnd. Výstup po dokončení vykresľovania vyzerá približne tak, ako na obrázku vľavo dole. Ak sa Vám na dokončenie simulácie nechce čakať, je možnosť vykresľovanie prerušiť pravým tlačidlom myši, alebo klávesou q, pričom dostanete podobý výstup ako na obrázku vpravo.

      

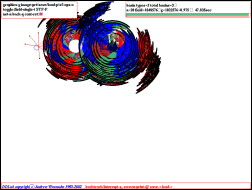
Na obrázku vľavo sú vykreslené všetky možné stavy siete v podobe čiernych krúžkov. Sú rozložené na sústredných kružniciach, ktorých stred prislúcha jednej oblasti atrakcie. V našom prípade má sieť tri atraktory; celý stavový priestor je teda rozdelený do troch množín (oblastí atrakcie) a tieto stavy sú vykreslené okolo troch rôznych stredov (Wuensche nazval túto sústavu grafov pole oblastí atrakcie). Stavy sú usporiadané podľa ich časovej nadväznosti smerom do stredu kružníc. Ak sa sieť nachádza v niektorom stave, po jednom stavovom prechode sa ocitne v stave, ktorý je s týmto spojený čiarou a leží bližšie ku stredu kružníc. Tento graf sa nazýva graf stavových prechodov. Z grafu stavových prechodov sa dá vyčítať niekoľko užitočných informácií. Ale keďže celkový počet stavov je v našom prípade 1 048 576, je logické, že sa na ploche 800x600 bodov mnohé z nich prekrývajú. Graf je teda dosť neprehľadný a preto DDLab ponúka množstvo možností jeho vykreslenia. Niektoré z nich si ukážeme o chvíľu; teraz sa pozrieme, čo sa dá vyčítať z grafu, ktorý práve máme:

• počet atraktorov - odpovedá počtu ustálených správaní simulovanej chemickej sústavy (bunky);
• veľkosť atraktorov - počet ich stavov. Tento údaj sa môže interpretovať ako počet chemických zmien v bunke počas jej životného cyklu (predpokladajme, že zdravá bunka sa po prejdení všetkých stavov atraktora rozdelí na dve totožné bunky). Z grafov je vidieť, že prvý atraktor má iba jeden stav (tu bude asi sústava v chemickej rovnováhe, t.j. bunka bude mŕtva), druhý atraktor má 15 a tretí 9 stavov, t.j. ak sa bude sústava nachádzať v týchto atraktoroch, bunka prejde v jednom životnom cykle 15 (9) chemickými zmenami;
• veľkosť oblastí atrakcie jednotlivých atraktorov si môžeme preložiť v našom prípade ako mieru homeostatickej stálosti bunky. To znamená, že čím väčšia je oblasť atrakcie, tým väčšia je šanca, že nejaké chemické vychýlenie bunky od normálneho stavu nebude mať za následok zmenu jej ustáleného správania. Tento poruchový stav sa bude nachádzať v tej istej oblasti atrakcie a po niekoľkých okamihoch sa bunka vráti do toho istého atraktora;

V pravom hornom rohu sa po skončení simulácie objaví informačné okno s nasledujúcimi údajmi: basin types - počet druhov oblastí atrakcie, total basins - celkový počet oblastí atrakcie, n - rozmer siete, field - veľkosť stavového priestoru (druhá mocnina rozmeru siete), g - je počet listových uzlov grafu (stavov bez predchodcocv (garden-of-eden states - rajských stavov)), kde druhý údaj predstavuje zlomok z celkového počtu stavov od 0 po 1. A nakoniec čas trvania kreslenia grafu.