Prírodou inšpirované algoritmy

Príklady priestoročasových obrazcov

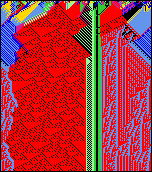
Na nasledujúcich obrázkoch máte možnosť vidieť priestoročasové obrazce 1D CA s n=150, k=4 a v=8. Vo všetkých prípadoch je použité všeobecné Altenbergove pravidlo, kde pravdepodobnosť výstupov vyhľadávacej tabuľky pravidiel je rovná frekvencii hodnôt v ich susedstve. Počiatočné stavy sú generované náhodne.

            

            

            

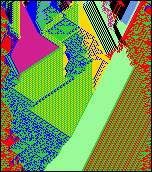
Nasledujúce série obrázkov znázorňujú "vývoj" 2D CA s zo súmerných pavidiel. Obrázky sú zoradené podľa časovej postupnosti zľava doprava, pričom prvý z nich predstavuje počiatočný stav siete v čase t=1. Tieto príklady názorne demonštrujú, že použitím súmerných pravidiel i počiatočných obrazcov, sa súmernosť siete zachováva. Prvá séria predstavuje 2D CA s n=50x50, k=4 a v=2 v časoch t=7,t=18 a t=35. 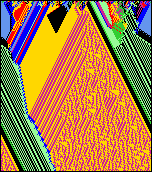Na druhej je 2D CA s n=50x50, k=5 a v=5 v časoch t=5, t=10 a t=23. Na tretej sérii obrázkov máte možnosť vidieť 2D CA s n=50x50, k=6 a v=5 v čase t=5, t=10 a t=20, v hexagonálnej mriežke.

                  

                  

                  

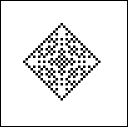
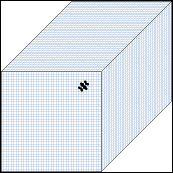
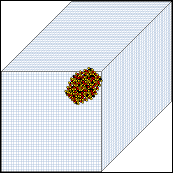
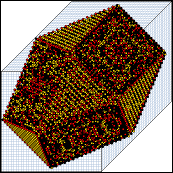
Posledný príklad "evolúcie" súmerných pravidiel môžete vidie na obrázkoch nižšie. Zachytávajú 3D CA s n=40x40x40 v=5 k=7 v čase t=1, t=10, t=25 a t=40.

      

      

Nasleduje príklad priestoročasového obrazca 1D CA s n=150, k=2, v=8, ktorý je generovaný súmerným pravidlom. Počiatočný stav je jedna 6-tka (tmavomodrá) v rovnomernom pozadí zo 7-čiek (čierna). Spolu je na obrázkoch znázornených 1153 časových krokov (obrázky na seba nadväzujú). Šiesty obrázok zachytáva, že sieť dosahuje atraktor tvorený samými nulami (svetlozelená). Toto pravidlo je súmerné a legálne, kde "súmerné" znamená, že zodpovedajúci susedia majú rovnaký výstup v tabuľke pravidiel (opakujú farbu) a "legálne" (podľa Wolframa) znamená súmerné pravidlo, ktoré pre okolia s rovnakou farbou nastaví túto farbu na výstupe (napr. 000->0, 111->1, 222->2). Príklad tiež ilustruje ďalšiu novú funkciu mvDDLab-u. Ide o vychyľovanie obrazca pre k=2 (resp. pre ľubovoľné párne k) rotáciou za sebou idúcich riadkov o 1/2 šírky bunky. Toto udržuje výskyt súmernosti pre párne k a robí systém ekvivalentný trojuholníkovej mriežke.

            

            

Posledná séria obrázkov zachytáva prvých 170 krokov pre rôzne 1D CA. Počiatočné stavy i pravidlá sú generované náhodne. Na obrázku vľavo dole je 1D CA s n=150, k=3 a v=3. Nasleduje 1D CA s n=150, k=2 a v=4. Na treťom obrázku je 1D CA s n=150, k=3 a v=4. Posledný obrázok znázorňuje 1D CA s n=150, k=2 a v=5.