Prírodou inšpirované algoritmy

Súvislosť s Fibonacciho postupnosťou

V dotykových parastichných sktutkovniciach sa vyskytujú čísla Fibonacciho postupnosti a divergenčný uhol (uhol medzi nasledujúcimi listami, v priemete zhora) blízky Fibonaccimho uhlu 137,51 stupňa. Ďaľšie často sa vyskytujúce uhly sú: 99,50 stupňa a 77,96 stupňa, kde parastichné skrutkovnnice obsahujú čísla: 1, 3, 4, 7, 11, ..., respektíve 1, 4, 5, 9, 14, .... Tieto postupnosti sú vyjadrené vzťahom:
un=un-1+un-2.

Matematické vysvetlenie

Zlomok(časť) reťazca (continued fraction) je zlomok, ktorý ma tvar

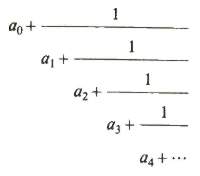
Kde a0, a1, a2, ..., an, ... sú reálne čísla. Všetky, až na možnú výnimku a0, sú kladné. Zapíšeme ich v tvare [a0;a1,a2,…]. Čísla an sa nazývajú čiastkové podiely zlomku. Ak je konečný počet nenulových čiastkových podielov, zlomok reťazca je konečný a ak sú naviac ešte prirodzené čísla, tento zlomok je jednoduchý. Konečný zlomok reťazca získaný z nekonečného, odrezaním všetkých členov za n-tým čiastočným podielom, an, sa volá n-tý konvergent zlomku reťazca. Označuje sa Cn.

Kde

Pk a qk majú tú vlastnosť, že ku konvergentu sa dostaneme už pri ich malých hodnotách. Ak a0=0 a ak=1 pre všetky ak>0, potom rekurentý vzťah pre pk a q<k vygeneruje Fibonacciho postupnosť a nasledujúce konvergenty (konvergujúce hodnoty) budú Cn=un+1/un, kde un reprezentuje n-té Fibonacciho číslo.

Každé racionálne číslo môže byť zapísané ako konečný zlomok reťazca dvoma navzájom súvisiacimi spôsobmi. Každé iracionálne číslo môžeme reprezentovať nekonečným zlomkom reťazca. Dôležitosť zlomku reťazca je, že ak vyjadríme pomocou neho iracionálne číslo x , potom konvergenty pn/qn najpresnejšie aproximujú x zo všetkých racionálnych čísel, ktorých menovateľ je rovný alebo menší qn.

Fibonacci v rastlinách

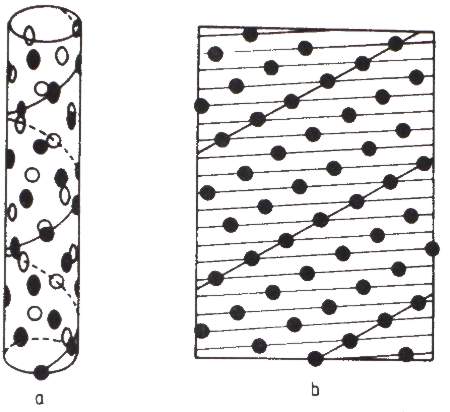
Ľavý obrázok je bočný pohľad na idealizovanú stonku. Vpravo je jej ekvivalent v rovine. Kontaktné parastichné čísla sú 3 a 5. Na obrázkoch je znázornená aj základná skrutkovnica, aj parastichná skrutkovnica 3 rádu.

Ak je daná kompletná množina dotykových parastichných čísel, môžeme vyrátať divergentý uhol riešením rekurentého vzťahu pre a1. V tomto konkrétnom príklade, ak pk= uk, potom zlomok reťazca je [0, 1, 1, 1, …], čo sa rovná (1+√5)/2, a to je približne 1.618. ( un+1/un s vyššími hodnotami konverguje k tejto hodnote). 2π (360 stuňov) predstavuje celý obvod kruhu, čiže 1. A tak 1.618 predstavuje uhol o hodnote 582.5 stupňa. Ten je totožný s uhlom 137.5 stupňa. A preto, ak na rastline medzi dvoma susediacimi (najbližšími) listami je tento uhol, kontaktné parastichné čísla, budú vždy z Fibonacciho postupnosti. Ak prirátame dané jedno parastichné číslo n, k nejakému listu l, a potom opäť k listu n+l a budeme takto pokračovať, dostaneme jednu konkrétnu špirálu. Ak k listu l budeme priratávať iné n, ale z Fibonnaciho postupnosti, dostaneme ďalšiu, inú parastichnú skrutkovnicu. Uhol 137.5 stupňa je Fibonacciho uhol.

Ak je uhol medzi susednými listmi 99.5 alebo 77.96 stupňa. Dostaneme podobné špirály podľa postupností [1, 3, 4, 7, …] respektíve [1, 4, 5, 9, .....].