Prírodou inšpirované algoritmy

Využitie L-systémov pri modelovaní vývinu rastlín

Základné princípy

L-systémy boli pôvodne predstavené na modelovanie vývinu jednoduchých viacbunkových organizmov so zameraním na delenie, rast a smrť jednotlivých buniek. Následne sa rozsah aplikácií L-systémov rozšíril na vyššie rastliny a zložité vetvené štruktúry (napr. súkvetia), ktoré možno opísať ako určitú konfiguráciu modulov v priestore. Modulom môžeme označiť ľubovoľnú diskrétnu konštrukčnú jednotku, ktorá sa počas vývinu rastliny opakuje, napr. rastový vrchol, časť stonky medzi kolenami, kvet alebo vetva. Cieľom modelovania na modulárnej úrovni je opísať vývin rastliny ako celku, so zameraním sa na emergenciu tvaru rastliny ako integráciu vývinu jednotlivých konštrukčných jednotiek.

L-systémy majú jednu veľkú výhodu: jednoduché L-systémy s malým počtom pravidiel dokážu opísať veľmi zložité objekty. Avšak napriek stručnosti L-systémov ich konštrukcia nie je triviálna úloha. Jedným z prístupov k modelovaniu rastlín je aj metodológia založená na simulovaní vývinu reálnych rastlín, teda ide o snahu zachytiť podstatu vývinového procesu, ktorý vedie k určitej forme. Tento vývinový prístup k modelovaniu rastlín má nasledovné charakteristické vlastnosti:

1. Dôraz na priestorovo-časové vzťahy medzi časťami rastliny. Na mnohých rastlinách možno naraz pozorovať rôzne vývinové štádiá. Napríklad niektoré kvety môžu byť ešte v štádiu púčiku, zatiaľ čo iné sú plne rozvinuté a ďalšie sú už premenené na ovocie.
2. Prirodzená schopnosť simulácie rastu. Keďže celý vývinový proces je opísaný matematickým modelom, môže byt použitý na generovanie biologicky korektných obrázkov rastlín v rôznom veku a na vytvorenie animácií rastu rastliny.

Riadiace mechanizmy v rastlinách

Predpokladajme, že chceme modelovať jednoduchú rastlinu s nerozvetvenou stonkou, z ktorej vyrastajú listy a s jedným kvetom na vrchole stonky. Tento model môžeme opísať nasledujúcim L-systémom:

Axiom = a
a → I [L] a
a → O [L] A
A → K

Symbol a reprezentuje rastový vrchol. V priebehu vývinu rastliny produkuje tento rastový vrchol v každom derivačnom kroku jeden nový segment stonky reprezentovaný symbolom I a jeden list reprezentovaný symbolom L ( pravidlo p1 ). V nejakom okamžiku vývinu sa rastový vrchol a premení na zárodok kvetu reprezentovaný symbolom A ( pravidlo p2 ) a ten sa v nasledujúcom derivačnom kroku prepíše na symbol K reprezentujúci kvet ( pravidlo p3 ). V biológii sa riadiace mechanizmy delia do dvoch tried v závislosti na spôsobe prenosu informácie:

1. rodové (lineage) - sú založené na prenose genetickej informácie z rodičovskej bunky na jej potomkov. Tieto sa dajú reprezentovať bezkontextovými pravidlami v 0L-systémoch.
2. interaktívne mechanizmy - pri nich dochádza k výmene informácie medzi susediacimi bunkami, čo vyžaduje použitie kontextových L-systémov.

Modely rastlinných orgánov

Príkazy pre korytnačku uvedené dosiaľ umožňovali vytvárať iba obrazce skladajúce sa z úsečiek. V nasledujúcej kapitole sa budeme venovať modelovaniu rastlinných orgánov pomocou plôch a rovinných polygónov.

Vkladanie predom definovaných plôch

Štandardná metóda počítačovej grafiky využíva pre definovanie povrchov bikubické plochy. Plocha je definovaná troma polynómami tretieho stupňa s parametrami s a t. Každú vkladanú plochu budeme reprezentovať jedným symbolom abecedy systému. Naviac rozšírime množinu príkazov pre korytnačku o symbol tilda ~. Ak korytnačka pri interpretácii reťazca narazí na tento symbol, vloží do obrazca preddefinovanú plochu reprezentovanú symbolom, ktorý v reťazci nasleduje. Presná pozícia a orientácia vkladanej plochy S sa určí pomocou kontaktného bodu PS a dvoch kolmých vektorov HS a US, ktoré musia byť určené pre každú vkladanú plochu. Plocha sa posunie a otočí tak, aby platilo:

PS = PT
HS = H
US = U


kde PT je pozícia korytnačky, a vektory H a U sú dva z troch vektorov určujúcich orientáciu korytnačky. Výhodou tejto metódy je možnosť vytvárania veľmi verných modelov rastlinných orgánov. Nevýhodou je však nesúlad s filozofiou L-systémov. Ten sa prejavuje napríklad v tom, že tieto plochy sa nemôžu vyvíjať rovnako ako iné časti modelu. Ak potrebujeme modelovať vývin takto generovaných častí rastliny, musíme pre každý vývinový stupeň vytvoriť zvláštnu plochu a každý krok vývinu modelovať vložením príslušnej plochy.

Vyvíjajúce sa modely

Predom definované plochy "nerastú". Pri ich vkladaní môžeme meniť ich veľkosť alebo farbu, ale ich tvar ostáva nezmenený. Ak chceme plne modelovať vývin rastliny, je nevyhnutné mať k dispozícii mechanizmus na zmenu nielen veľkosti, ale aj tvaru plôch v čase. Jednou možnosťou je prejsť obrysy plochy s korytnačkou a vzniknuté polygóny vyplniť. Pre tento účel zavedieme ďalšie nové príkazy pre korytnačku:

{ - iniciuje mód vytvárania polygónu. Po každom kroku vyvolanom príkazom 'F' alebo 'f' bude pozícia korytnačky zaznamenaná ako ďalší vrchol práve vytváraného polygónu.
} - ukončí mód vytvárania polygónu. Zaradí do obrazca polygón určený zaznamenanými vrcholmi.
G - má rovnaký význam ako príkaz 'F', ale pozícia korytnačky nie je zaznamenaná ako vrchol polygónu.
g - má rovnaký význam ako príkaz 'f', ale pozícia korytnačky nie je zaznamenaná ako vrchol polygónu. Zaznamená aktuálnu pozíciu korytnačky ako vrchol polygónu.

Pre vytváranie polygónov sa používajú dve základné metódy. Prvou z nich je pomocou príkazov 'F' a 'f' obísť s korytnačkou po obvode polygónu a tak zaznamenať všetky jeho vrcholy. Druhá možnosť je pohybovať sa s korytnačkou pomocou príkazov 'G' a 'g' po akejsi kostre polygónu, skladajúcej sa napríklad z niektorých jeho uhlopriečok a jeho vrcholy zaznamenať pomocou príkazu '.'. Ak chceme generovať plochu so zložitejším okrajom alebo plochu, ktorá nie je rovinná, je výhodnejšie vygenerovať stromovú štruktúru, ktorá bude tvoriť kostru plochy a vrcholy polygónu definovať pomocou príkazu '.'. Týmto spôsobom je možné pomocou množiny polygónov generovať aj pomerne zložité plochy.

Modifikujme význam príkazov '{' a '}'. Príkaz '{' uloží práve vytváraný polygón na zvláštny zásobník ( iný ako zásobník na ktorý sa ukladajú stavy korytnačky ) a ako aktuálny bude vytvorený nový prázdny polygón. Príkaz '}' uzavrie aktuálny polygón, zaradí ho do generovaného obrazca a vyberie z vrcholu zásobníku polygón, ktorý sa stane aktuálnym. Tento spôsob interpretácie príkazov umožňuje vnáranie polygónových zátvoriek '{' a '}' v reťazci. Z týchto trojuholníkov sa skladá celý list. Na obrázku je zobrazený vývin tohto listu:

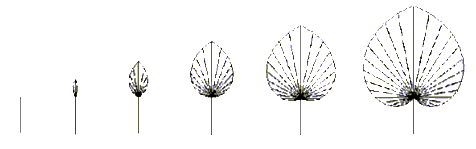
Modely zložených listov

Doteraz sme sa zaoberali modelovaním rastlinných orgánov pomocou plôch a polygónov. Ak však chceme generovať niektoré zložité, sebepodobné štruktúry, napríklad listy papradia a podobne, nie je táto metóda príliš vhodná vzhľadom k veľkej členitosti týchto plôch. Pri generovaní týchto plôch sa vrátime k obrazcom zloženým z úsečiek. Nasledujúci L-systém generuje rôzne tvary listov papradia v závislosti na hodnotách konštánt D a R:

Axiom = A(0)
α = 45°
A(p) : p>0 → A(p-1)
A(p) : p=0 → F(1) [+A(D)] [-A(D)] F(1) A(0)
F(a) → F(R*a)

Na obrázku je päť listov vygenerovaných týmto L-systémom:

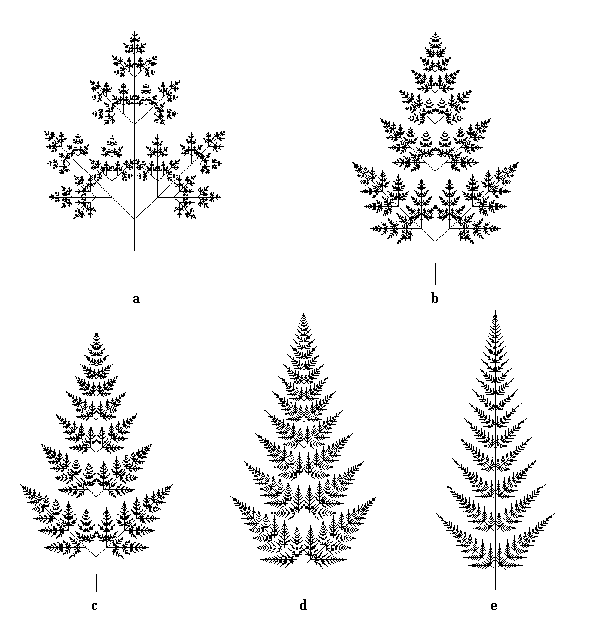
Tropizmus

Vyššie opísané nástroje pre modelovanie rastlín popisujú tvar rastliny relatívne k počiatočnému stavu korytnačky. Avšak pri vývine rastlín obvykle hrajú určitú úlohu aj absolútne smery. Smer rastu rastliny je ovplyvňovaný gravitáciou (geotropizmus), natočenie listov býva závislé na smere k hlavnému zdroju svetla (fototropizmus), atď. Tieto vplyvy je možné modelovať nasledovným spôsobom. Je daný vektor T určujúci smer tropizmu (smer, do ktorého je rastlina "priťahovaná"). Každý segment, ktorý vkladáme do modelu, natočíme smerom k tomuto vektoru o uhol a, ktorého veľkosť je možné vyjadriť vzťahom a = | e.S ´ T | , kde e je elasticita segmentu a vektor S popisuje smer a dĺžku segmentu. Tento heuristický vzorec má fyzikálnu motiváciu: ak T je interpretované ako sila pôsobiaca na koncový bod vektora S a S sa môže otočiť okolo svojho počiatočného bodu, uhol otočenia je úmerný | S ´ T |.