Prírodou inšpirované algoritmy

Model s dvoma jazdnými pruhmi

Model s dvoma jazdnými pruhmi rovnakého smeru

Pri uvažovaní o prípade kedy máme viac ako jeden jazdný pruh, musíme implementovať symetrický model zmeny jazdných pruhov, kde vozidlá nemajú žiaden predom určený jazdný pruh. Pred zmenou jazdného pruhu musí vozidlo preveriť dve hodnoty gap a to pred sebou a gap za sebou na jazdnom pruhu kam sa chce presunúť aby sa tak predišlo nehode.

Ak uvažujeme model v ktorom sú obe jazdné pruhy orientované rovnakým smerom hovoríme potom o paralelných CA modeloch s jedným jazdným pruhom.

Pre potreby popísania procesu výmeny vozidiel medzi jazdnými pruhmi je potrebné pridať ďalšie pravidlá a zároveň sú zavedené aj nové premenné a to: gapsame(i), gapopposite(i) popisujúce počet neobsadených pozícií pred vozidlom na oboch jazdných pruhoch resp. premenná gapbehind označuje počet neobsadených pozícií za vozidlom v druhom jazdnom pruhu. Ďalej sú potrebné premenné lsame, lopposite, lback označujúce minimálnu voľnú vzdialenosť potrebnú na obiehanie vpredu a vzadu v opačnom jazdnom druhu a vpredu v aktuálnom jazdnom pruhu. Premenná pchange označuje pravdepodobnosť zmeny jazdného pruhu.

Na základe definovania týchto premenných môžeme pridať nasledujúce pravidlo:

IF (gapsame(i) < lsame) AND (gapopposite(i) > lopposite) AND (gapbehind (i) > lback ) AND (rand < pchange) THEN change lane

U tohoto modelu môžeme hovoriť o symetrickej resp. asymetrickej verzii. Pri asymetrickej verzii nie je povolené obiehanie po pravej strane.

Model s dvoma jazdnými pruhmi obojsmerný

V tejto oblasti existuje viacero podtypov modelov. Model napríklad povoľuje obiehanie na oboch jazdných pruhoch, obiehanie je povolené len v rámci jedného jazdného pruhu resp. je obiehanie úplne zakázané. Najviac sa samozrejme realite podobajú modely, ktoré spájajú tieto možnosti a vytvárajú tak úseky cesty implementáciou rôznych podtypov.Uvažujme teda o modeli, ktorý povoľuje obiehanie.

Algoritmus kontrolujúci obiehanie musí zobrať do úvahy rad okolností. Medzi ne patrí napr. fakt, že vozidlo si musí počas obiehania udržať konštantné zrýchlenie ( p je počas obiehania nastavené na 0 ). V prípade, že je detekované blížiace sa vozidlo v obiehacom jazdnom pruhu, obiehajúce auto sa musí urýchlene vrátiť do svojho jazdného pruhu. Daný model by mal zohľadňovať aj istú racionalitu vodičov v realite, a to tým, že vozidlo sa nebude pokúšať o obiehanie v prípade, že obiehanie nie je možné dokončiť.

Na zistenie šance, že vozidlu bude umožnené dokončiť obiehací manéver a teda, že samotné obiehanie bude povolené slúži lokálna hustota. Táto hodnota popisuje hustota (množstvo) vozidiel pred daným vozidlom, ktoré chceme obiehať. Pri modeli s obojsmernou premávkou sa môžu vyskytnúť tri druhy zabrzdenia premávky. Prvý a najčastejší z nich je tzv. štart-stop vlna na jednom z jazdných pruhov. Druhý je spôsobený príliš odvážnymi “ vodičmi “, ktorý sa pokúšajú o obiehanie aj napriek tomu, že nemajú miesto na návrat do svojho pôvodného jazdného pruhu. K tomuto prípadu však nedochádza často. Posledným a dá sa povedať, že aj najväčším problémom je ak sa pár susediacich vozidiel (obsadzujú teda obe jazdné pruhy) rozhodne obiehať súčasne. Týmto však zastavia premávku v oboch smeroch.

Aby sa predišlo spomínaným problémom sú v tomto modeli použité nasledujúce pravidlá a konvencie. Rovnako ako je tomu pri modeli s jedným jazdným pruhom, tak aj tu sú jednotlivé bunky označené hodnotou premennej v {-(vmax + 1) ... vmax +1}, pričom 0 reprezentuje neprítomnosť vozidla na danej pozícii, ±1 označuje stopnuté vozidlo, ±2 označuje vozidlo pohybujúce sa rýchlosťou 1 dopredu resp. dozadu atď. Týmto spôsobom je možné označiť oboje, vozidlá aj jazdné pruhy znamienkami “ + “ a “ - “. Vozidlo so znamienkom “ + “pohybujúce sa na jazdnom pruhu označenom “ + “ sa teda pohybuje po svojom domovskom jazdnom pruhu. Vozidlo so znamienkom “ + “ na jazdnom pruhu “ - “ sa nachádza na obiehacom jazdnom pruhu. Analogicky to platí pre vozidla so znamienkom “ - “. Výpočet pohybu vozidiel je realizovaný v dvoch krokoch. V prvom kroku vozidlo zmení jazdný pruh.Je potrebné si zaviesť ďalšie označenia:

• sign(): znamienko
• not(): logická negácia
• vsame, vopposite: rýchlosť vozidla vpredu na rovnakom resp. opačnom jazdnom pruhu
• H: má hodnotu true ak sa vozidlo nachádza na pôvodnom jazdnom pruhu
• oncoming: má hodnotu true ak platí sign( vsame ) ≠ sign ( v )
• lpass: ak gapsame < lpass AND H potom sa môže pokúsiť o obiehanie
• lsecurity: ak gapsame < lsecurity AND not( H ) potom sa vozidlo okamžite vracia do pôvodného jazdného pruhu
• DL: lokálna hustota: zlomok ldensity = 2 x vmax + 1 obsadených pozícií pred daným vozidlom
• Dlimit: maximálna lokálna hustota umožňujúca bezpečné obiehanie

O zmene jazdných pruhov sa rozhoduje na základe nasledujúcich pravidiel:

1. IF ( H AND ( gapsame < lpass ) AND ( gapopposite > lsecurity ) AND ( DL ≤ Dlimit ) AND ( rand < pchange )) THEN change lane
2. If ( not(H) AND (( gapsame < lsecurity ) OR ( gapopposite ≥ lpass ))) THEN change lane

Prvá podmienka ovplyvňuje vozidlá na ich domovskom ( pôvodnom ) jazdnom pruhu. Ak je vozidlo pred nim vo vzdialenosti menšej ako lpass, potom bude obiehať toto vozidlo, avšak len vtedy ak je pred obiehaným vozidlom dostatok voľného miesta a zároveň tam nesmie byť veľa iných vozidiel, ktoré by musel tiež obehnúť.

Obiehanie je iniciované náhodne a dokonca aj pri splnení všetkých spomenutých podmienok je pravdepodobnosť, že dôjde k zmene jazdného pruhu vyjadrená hodnotou premennej pchange.

Druhá podmienka sa zameriava na riadenie vozidla počas procesu obiehania. Vozidlo sa musí vrátiť do svojho pôvodného jazdného pruhu vtedy ak sa blíži oproti idúce vozidlo, alebo vtedy ak v pôvodnom jazdnom pruhu je dostatok miesta na to aby sa tam vrátilo bez brzdenia.

Predpokladajme teda situáciu, kde oboje oproti idúce vozidlá chcú obiehať súčasne. Na základe predchádzajúcich podmienok, si obe vozidlá udržia svoju rýchlosť ( nedôjde teda k náhodnej zmene rýchlosti ) a zároveň vozidlá v ich pôvodných jazdných pruhoch zredukujú svoju rýchlosť o jedna, čím sa vytvoria voľné miesta pre obe obiehajúce vozidlá a tie sa môžu vrátiť do svojich jazdných pruhov.

Pohyb vpred je popísaný nasledovnými pravidlami:

1. IF ( |v| ≠ vmax ) THEN v = v + sign( v )
2. IF (( oncoming ) AND ( gapsame ≤(2 x vmax -1 ))) THEN v = | gapsame/2 |
3. IF (( not(oncoming )) AND ( |v| > gapsame )) THEN v = sign( v ) x gapsame
4. IF (( H AND ( |v| > 1 ) AND ( rand < pdeceleration ) AND not( oncoming )) THEN v = v – sign( v)
5. IF ( H AND ( oncoming ) AND ( |v| > 1 )) THEN v = v – sign( v )

Jednotlivé pravidlá vykonávajú:

1. akcelerácia vozidla na maximálnu rýchlosť
2. rýchle brzdenie vozidla ak je oproti idúce vozidlo príliš blízko
3. brzdenie vozidla ak je príliš blízko iného vozidla, pričom oboje sa nachádzajú na domovskom jazdnom pruhu
4. náhodne brzdenie, môže nastať len ak sa vozidlo nachádza na domovskom jazdnom pruhu
5. rušenie symetrickosti medzi jazdnými pruhmi a tak zabránenie vyššie popísanému problému číslo tri (dve súčasne obiehajúce vozidlá )

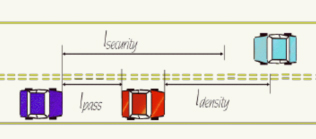
Popisovaný CA model pre dva jazdné pruhy s obojsmernou premávkou predstavuje túto reálnu situáciu

Typický priestorovo-časový diagram

Časť cesty obsahujúca vozidlo pohybujúce sa doprava na svojom domovskom jazdnom pruhu je označené červenou. Vozidlo pohybujúce sa doľava po svojom domovskom jazdnom pruhu je označené zelenou farbou. Ďalšie možné situácie sa označujú ďalšími farbami ako napríklad obiehajúce vozidlo idúce doprava ( tmavo modrá ). Na vľavo - idúcom jazdnom pruhu je hustota blízka kritickej pre zápchy (0.1) a nízka hustota je naopak na pravo – idúcom jazdnom pruhu (0.01). Na nasledujúcom obrázku je možné pozorovať ako premávku ovplyvňuje možnosť obiehania.

Situácia je podobná ako na predchádzajúcom obrázku, avšak v tomto prípade bola cesta rozdelená na časť v ktorej obiehanie bolo povolené ( ľavá polovica obr. ) a časť kde bolo obiehanie zakázané ( pravá polovica obr. ). Ako je vidieť, na ceste kde nebolo obiehanie povolené sa častejšie vyskytovali zápchy.

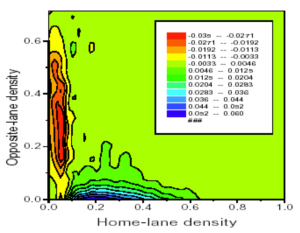
Grafické znázornenie premávky na domovskom jazdnom pruhu

Premávka na domovskom jazdnom pruhu je graficky znázornená ako funkcia hustoty na domovskom a opačnom jazdnom pruhu. Farby tu udávajú rozdiel medzi premávkou na domovskom jazdnom pruhu v modeli s dvomi jazdnými pruhmi s obojsmernou premávkou s možnosťou obiehania a premávkou na modeli s jedným jazdným pruhom s porovnateľnou hustotou. Obrázok naznačuje, zanedbateľný rozdiel medzi modelom s jedným a dvomi jazdnými pruhmi. Aj napriek tomu sú tu viditeľné dve základné črty: 1) zväčšená premávka ak je hustota na oproti idúcom jazdnom pruhu nízka, a 2) znížená premávka ak je hustota v domovskom jazdnom pruhu nízka a zároveň hustota na opačnom jazdnom pruhu je relatívne vysoká. Tento posledne menovaný efekt je spôsobený obiehaním oproti idúcich vozidiel, ktoré tak zasahujú do premávky v domovskom jazdnom pruhu.

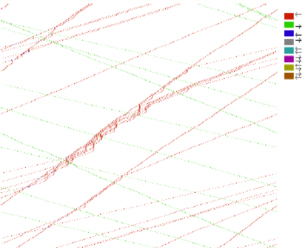
Viacrýchlostný variant

Pri tomto variante majú vozidlá maximálne rýchlosti, rovnomerne rozložené medzi 2 a 5. V strednej časti je znázornená časť cesty so zákazom obiehania. Po okrajoch je obiehanie povolené. Pomalé vozidlá vykresľujú strmšie čiary. Treba si tu všimnúť uzol vozidiel v blízkosti stredu diagramu, ktorý je vytvorený pomalým vozidlom ( idúcim doľava ) a vstupujúcim do oblasti so zákazom obiehania. Akonáhle uzol opustí hranicu tejto oblasti, dopravná zápcha sa rozplynie. Tieto priestorovo - časové diagramy dokazujú, že tento model dokáže korektne simulovať správanie sa reálnej premávky. Modelovanie topograficky realistických ciest, je možné dosiahnuť napr. kombináciami oblastí s povoleným resp. zakázaným obiehaním, ktoré boli spomenuté vyššie a tak simulovať zákruty apod.