Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
CA 1.1
Howard Gutowitz vyvinul kryptosystém pomenovaný CA-1.1, ktorý demonštruje niektoré princípy šifrovania využívajúc celulárne automaty. V tomto systéme je správa šifrovaná ako stav systému, na ktorý sú aplikované rôzne pravidlá celulárneho automatu za účelom vyprodukovania nového stavu, ktorý bude predstavovať šifrovaný text (ciphertext). Na dešifrovanie sa použijú rovnaké pravidlá celulárneho automatu, ale v opačnom poradí.
CA-1.1 využíva vratné a nevratné pravidlá 1D celulárneho automatu. Pri vratnom pravidle (reversible rule) pochádza každý stav mriežky z jedinečného predchodcu stavu, zatiaľ čo pri nevratnom pravidle (irreversible rule) môže mať každý stav veľa predchodcov stavov.
Tento systém používa ako dopredné, tak aj spätné iterácie pre šifrovanie a dekódovanie. Spätná iterácia nevratného dynamického systému vytvára dynamický vstup/výstup, ktorý môže byt použitý pre šifrovanie informácie. Príčinou prečo nebola spätná iterácia tohto nevratného dynamického systému použitá v nejakom reálnom systéme je, že nevratný dynamický systém má obyčajne niekoľko možných predchodcov stavov. Tým hlavným problémom ale bolo, ktorý z týchto niekoťkých stavov použiť a ako potom zistiť, ktorý bol použitý. Tento stav môže byť vybratý náhodne alebo podľa informácie vloženej do vstupného prúdu informácie. Ak je vybratý náhodne, potom táto náhodnosť môže viesť k náhodným údajom aj pri šifrovaní správy, a neskôr aj v samotnom šifrovanom texte. A to je spôsob ako znepríjemniť život tým, ktorý sa pokúšajú dekódovať našu správu. Akonáhle niekto vlastní klúč, podľa ktorého sme vyberali dynamický systém aj s pravidlom, ktoré sme použili na kódovanie (a určili, ktorý z náhodnýsh stavov sa použije), potrebuje ho už iba použit na šifrovaný text. Keďže pri šifrovaní sa použila spätná iterácia, na dešifrovanie sa použije dopredná a následne dostaneme pôvodný text. Cieľom tejto doprednej iterácie je odstrániť náhodný text, ktorý bol k správe pridaný počas šifrovania.
Spätná iterácia takto slúži k zmiešaniu náhodnej informácie so skutočnou informáciu v správe a môže byť použitá aj niekoľko krát za sebou, čo sa aj využíva. CA-1.1 používa špeciálny druh čiastocne lineárneho nevratného pravidla, ktoré umožnuje to, aby mohol byť náhodný predchodca stavu (pre ktorýkoľvek daný stav) rýchlo postavený. Vratné pravidlá sa taktiež používajú pre niektoré fázy šifrovania. Sú plne nelineárne, zatiaľ čo nevratné pravidlá sú čiastocne lineárne. Nevratné pravidlá sú získané len z informácie v klúči, kým vratné pravidlá závisia ako od informácie v klúči, tak aj od náhodnej informácie vloženej počas fáz šifrovania s nevratnými pravidlami.
CA-1.1 využíva overovací mechanizmus, ktorý zaisťuje to, že zašifrovaný text môže byť dešifrovaný iba s použitím rovnakého klúča, s akým bol zašifrovaný.
CA-1.1 je postavený na blokovo-linkovacej štruktúre. To znamená, že spracovanie bloku správy je čiastocne oddelené od spracovania prúdu náhodnej informácie vloženej počas šifrovania. Táto náhodná správa slúži na linkovanie (spájanie) jednotlivých fáz šifrovania do jedného celku. Môže takisto slúžiť na spojenie šifrovania jednotlivých blokov dokopy. Táto informácia je generovaná vo vnútri šifrovacieho aparátu.
Charakteristika systému CA-1.1
- blokovo-linkový kryptosystém, ktorý využíva 384-bitové bloky a 320-bitové linky, kde správa, ktorá má byť zašifrovaná je zašifrovaná v blokoch a linky sú vygenerované zdrojom vo vnútri šifrovacieho aparátu. Dešifrovanie opätovne zostaví bloky a zničí linky.
- používa 1088-bitový klúč rozdelený na dve časti a to,
- blokový klúč o dlžke 1024bitov
- linkový klúč o dlžke 64bitov
- je navrhnutý tak, aby informácia o linke ostala utajená aj pred útokom typu chosen-plaintext. Dokonca nie je možné zistiť ani len inicializačnú linku informácie.
- využíva ako vratné(reversible), tak aj nevratné(irreversible) pravidlá Celulárnych Automatov. Nevratné sú špecifikované klúčom a vratné pravidlá sú generované z informácie linky.
- funkčne napodobňuje DES (Data Encryption Standart) vo vhodne zabezpečenom prostredí, využívajúc 64bitový klúč a (násobky) 64bitové bloky
Už vieme, že celulárne automaty používame ako tajné kľúče pre šifrovanie a dešifrovanie správ, ktoré majú zostať utajené pred nepovolané osoby. V našom názornom príklade použitia kryptosystému budeme mať dve banky (banka A a banka B), ktoré potrebujú vzájomne komunikovať a vymieňať si dôverné dáta. Skôr ako budú môcť vzájomne bezpečne komunikovať, musia si vymeniť tajnú kolekciu celulárnych automatov a nejakú konvenciu pre výber celulárneho automatu vybraného v danom kroku šifrovania/dešifrovania správy. Vždy sa vyberie iba jeden celulárny automat + celé číslo n, ktoré bude udávať počet opakovania krokov šifrovania/dešifrovania.
V tomto príklade sa banka A snaží poslať údaje o trasakciách banke B, pričom šifrovanie bude prebiehať prostredníctvom čísel reprezentujúcich hodnoty jednotlivých transakcií. Banka B musí presne identifikovať tieto čísla, kedže reprezentujú buď hodnotu v dolároch alebo jenoch, a tak je potrebná ešte reprezentácia pomocou kódov reprezentujúcich jednotlivé informácie. Zistili, že pre ich požiadavky vyhovuje 4-bitový binárny kód
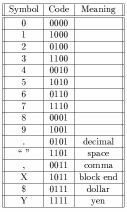
Kódy pre symboly použité pre komunikáciu medzi bankami
A ako vyzerá postup spracovania? V nasledujúcich riadkoch je uvedený "hrubý" popis činnosti.
Informácia, ktorá má byť zašifrovaná sa vezme z nejakého informačné prúdu, ktorý si označíme ako 100 a je vygenerovaný bankou A. Tento vstupný prúd je pred zašifrovaním uložený na nejakom mieste, napríklad na disku počítača. Tento informačný prúd obsahuje bankové informácie (symboly) nachádzajpce sa v predchádzajúcej tabuľke v prvom stĺpci. Banka A tiež vlastní aj generátor šumu resp. náhodných informácii 200. Banka A má kóder 300, ktoré je READ-ONLY pamäťou obsahujúcou informácie z prvej tabuľky. Banka A má samozrejme aj šifrovacie zariadenie 400, ktoré je schopné spätnej iterácie s daným celulárnym automatom potrebnej na šifrovanie.. Banka B vlastní dešifrovacie zariadenie, schopné doprednej iterácie na danom celulárnom automate, rovnako vlastní dekódovacie zariadenie, ktoré dokáže preložiť prúd bitovej informácie do prúdu bankových symbolov.
Banka A chce teba poslať banke B správu "Y146.00". Obe banky zdieľajú jeden tajný kľúč (celulárny automat) využívajúci pravidlo 30, ktorého pravidlo je zaznačené v druhej tabuľke. Obe banky sa dohodli na tom, že sa pri ich komunkácii vykoná 14 krokov (n=14) šifrovania/dešifrovania.
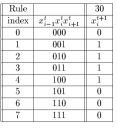
Iterácia celulárneho automatu pre pravidlo 30 použitého ako príklad kľúča
V tretej a štvrtej tabuľke je vidieť jednotlivé kroky tohto šifrovania/dešifrovania v dvoch možných formátoch. Tabukľa 3 zobrazuje stav pamäte po jednotlivých krokoch vo formáte, ktorý bol uvedený v prvom stĺpci prvej tabuľky. čo je vidieť ja na prvý pohľad. Naopak štvrtá tabuľka už tieto údaje nezobrazuje priamo, ale využíva už zmienený 4-bitový kódovy zápis následkom čoho aj čitateľnosť ešte nezašifrovanej správy je komplikovanejšia.
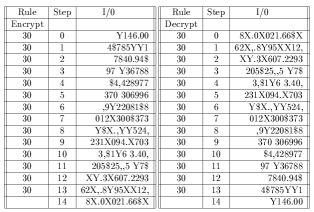
Táto tabúľka ukazuje ako sa zmení pôvodná informácia "Y146.00" na zašifrovaný text. Pri šifrovaní je v riadku 0 plvodný text a zašifrovaný text sa zobrazuje v 14. riadku ako 8X.0X021.66$X. U dešifrovania je to presne naopak.

