Prírodou inšpirované algoritmy

Architektúra

Vyznávači zlatého rezu hľadali oporu pre svoje tvrdenia v plánoch architektúr všetkých dôb i slohov. Najväčší pamätník zlatého rezu vidia niektorí bádatelia v Cheopsovej pyramíde.

Pomer plochy podstavy tejto pyramídy k ploche jej plášťa je rovný pomeru plochy plášťa k celému jej povrchu. Nech je c výška bočnej steny, a polovica strany podstavy, a h výška pyramídy, potom platí a : h = h : c. Uhol medzi podstavou a stenami pyramídy je 51°50´, čo je presne hodnota korešpondujúca s uhlom v trojuholníku o stranách 1, odmodcnina z 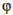a 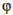(a, h, c). Tento trojuholník je jediný pravouhlý trojuholník so stranami, ktorých veľkosti tvoria geometrickú postupnosť. V skutočnosti je a : h = 0,785 a h : c = 0,786, čo je zhoda skutočne nápadná, ale jej predpoklady sú príliš umelé a neodpovedajú citu vtedajšieho obyvateľstva a stavu vtedajšej geometrie.

Starí Gréci zlatý rez poznali a architekti Itkinos a Kaligrates ho mohli použiť pri stavbe chrámu Parthenón na Akropole.

Parthenón je typický dórský chrám s ôsmimi stĺpmi spredu aj zozadu a je nepochybne najkrajším chrámom postaveným týmto štýlom. Do priečelí Parthenónu je možné nakresliť časť pravidelného desaťuholníka, ktorý má súvislosť so zlatým pomerom.

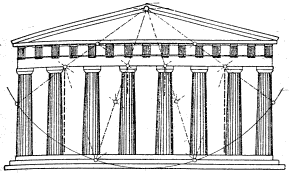
A nie iba tam. Na schéme pôdorysu tohoto monumentu možno nájsť ďalšie desaťuholníky vpísané sústredným kružniciam.

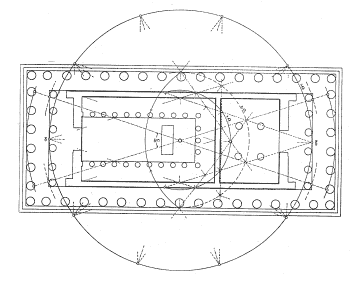
Gréci videli v číslach krásu a milovali ušľachtilé tvary. Svojich pokračovateľov našli i omnoho neskôr napr. v gotike pri stavbe chrámu Notre-Dame v Paríži, v kompozícii fasád chrámov ruskej architektúry 12. storočia, v dielach architekta Le Corbusiera alebo v architektúre budovy Organizácie spojených národov v New Yorku. Zlatý rez však nemožno dokázať všeobecne a nemožno hovoriť o jeho akejsi všeobecne platnej umeleckej prednosti pred inými proporciami.