Prírodou inšpirované algoritmy

Zlatý trojuholník

Rovnoramenný trojuholník, v ktorom je pomer dĺžky ramena a základne rovný 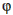, nazveme zlatým trojuholníkom.

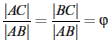
V zlatom trojuholníku sú uhly pri základni rovné 72° a uhol pri hlavnom vrchole 36°. Do daného trojuholníka ABC vpisujeme najväčšie možné rovnoramenné trojuholníky, ktoré majú rameno rovné základni predchádzajúceho trojuholníka. Opäť platí, že ostane zlatým trojuholníkom. Platí |AB|=|CD|, a po dosadení platí podľa definície zlatého rezu 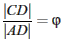, a pretože platí |CD|=|BD|, platí 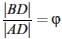, teda trojuholník ABD je zlatý.

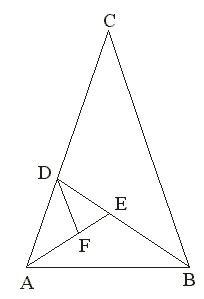
Logaritmickú špirálu je možné zostrojiť i pomocou zlatých trojuholníkov. Ich vrcholy ležia na špirále, ktorá má stred v priesečníku ťažníc AA1 a DD1. Stredy ich oskulačných kružníc ležia v bodoch D, E, F...