Prírodou inšpirované algoritmy

Výpočet zlatého pomeru

Aby sme sa dostali k spôsobu výpočtu zlatého pomeru, je potrebné vysvetliť, čo rozumieme pod pojmom zlatý rez.

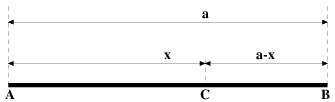
Ak rozdelíme úsečku AB dĺžky a bodom C na dve časti x a (a - x) tak, aby sa pomer dĺžok väčšej časti x k menšej časti (a - x) rovnal pomeru dĺžky úsečky a k väčšej časti x, teda aby platilo

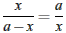
potom hovoríme, že sme zostrojili zlatý rez (bod C) úsečky AB a pomer a:x,
resp. x:(a - x), nazveme zlatým pomerom. Tento pomer označil americký matematik Mark Barr písmenom 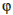podľa počiatočného písmena mena najslávnejšieho starovekého gréckeho sochára Feidia, ktorý vo svojich dielach zlatý rez používal. Hodnotu môžeme veľmi jednoducho určiť. Zvoľme veľkosť úsečky a = 1 a dosaďme do rovnice zlatého rezu:

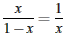
Po úprave riešime kvadratickú rovnicu

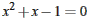
ktorej kladný koreň je

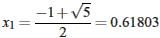
a pomer

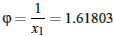
Záporný koreň nevyhovuje, lebo x je dĺžka úsečky. Jeho prevrátenú hodnotu -0,61803 nazveme 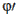a použijeme ho k odvodeniu zaujímavých vlastností čísla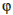

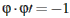
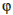má ďalšiu jedinečnú vlastnosť - je to jediné kladné číslo, ktoré zmenšené o jedničku dává svoju prevrátenú hodnotu

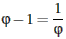
Tento vzťah dostaneme dosadením 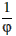za x do kvadratickej rovnice. Zlatý pomer môžeme vyjadriť dvoma zpôsobmi

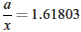
alebo