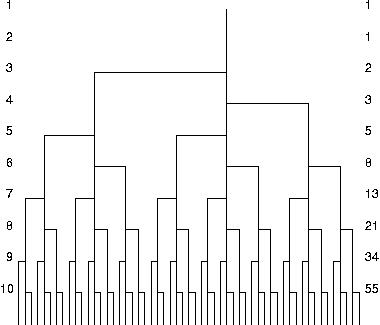Prírodou inšpirované algoritmy

Fibonacciho králiky

Taliansky matematik Fibonacci (1170 - 1230), pravým menom Leonardo Pisano, sa preslávil svojou knihou "Liber abacci", v ktorej zhrnul všetky vtedajšie znalosti o aritmetike a algebre. Bola to v Európe jedna z prvých kníh, ktorá učila používať desiatkové sústavy. Vtedajšie matematické znalosti objasňoval na mnohých úlohách, z ktorých sa úloha o králikoch zapísala do histórie matematiky tým, že dala podnet k vybudovaniu tzv. teórie Fibonacciho čísel.

Pôvodným problémom, ktorý Fibonacci skúmal (v roku 1202), pojednával o tom, ako rýchlo sa králiky dokážu v ideálnych podmienkach rozmnožovať.

Predpokladajme čerstvo narodený pár králikov, jedného samčeka, jednu samičku vypustených na pole. Králiky sú schopné mať potomstvo vo veku jedného mesiaca, takže na konci svojho druhého mesiaca môže samička "vyprodukovať" ďalší pár zajacov. Predpokladajme, že naše králiky nikdy nezahynú a že samička stále vyprodukuje jeden nový pár (jedného samčeka a jednu samičku) každý mesiac počnúc druhým mesiacom. Otázka znie:

Je zrejmé, že

1. na konci prvého mesiaca bude pár iba jeden
2. na konci druhého mesiaca samička vyprodukuje nový pár (už sú páry dva)
3. na konci tretieho mesiaca, pôvodná samička vyprodukuje druhý pár (spolu tri)
4. na konci štvrtého mesiaca vyprodukuje pôvodná samica ďalší nový pár, samica narodená pred dvoma mesiacmi vyprodukuje taktiež svoj prvý pár (dokopy päť)

Počet párov králikov na začiatku každého mesiaca je (viď tiež ďalší obrázok)