Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
Príklady fraktálov
Sierpinského trojuholník
Sierpinského trojuholník generovaný stochastickým algoritmom. Pod obrázkom sú rovnice zobrazení, ktoré postupne transformujú pôvodný bod.

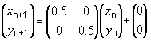
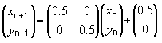
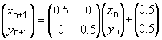
Je možné použiť aj nasledujúci algoritmus: v pôvodnom trojuholníku zvolíme ľubovoľný bod. Náhodne vyberieme jeden z vrcholov a posunieme zvolený bod smerom k nemu na polovičnú vzdialenosť a vykreslíme ho. Pre tento nový bod potom opakujeme celú procedúru. Výsledok je fantastický. Nikdy nevieme povedať, kde bude ďalší bod, no vždy to bude bod fraktálu. Postupne sa bude daný útvar zaostrovať.
Sierpinského päťuholník
Zmena v algoritme oproti predošlým je v tom, že sa používa 6 vrcholových bodov, na ktoré sa uplatní transformácia posunu. Náhodne vygenerovaný bod z vnútra päťuholníka bude bodom fraktálu, ak sa posunie na vzdialenosť približne 17/27 k vrcholu.

Sierpinského šesťuholník
Zmena v algoritme oproti predošlým je v tom, že sa používa 6 vrcholových bodov, pre ktoré sa používa transformácia posunu. Náhodne vygenerovaný bod z vnútra šesťuholníka bude bodom fraktálu, ak sa posunie na vzdialenosť 2/3 k vrcholu.

Sierpinského koberček
Zmena v algoritme oproti predošlým je v tom, že sa používa 8 vrcholových bodov, pre ktoré sa používa transformácia posunu. Náhodne vygenerovaný bod z vnútra šesťuholníka bude bodom fraktálu, ak sa posunie na vzdialenosť 2/3 k vrcholu.
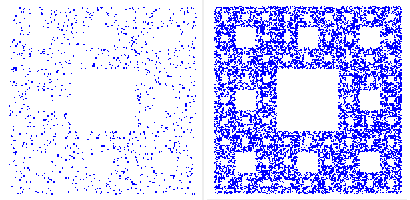
Kochova vločka
Základný princíp je v generovaní troch nových bodov medzi dvomi. Proces je graficky vysvetlený na nasledovnom obrázku:
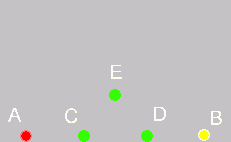
Pre výpočet súradníc bodov C, D, E sa používajú nasledovné vzťahy: používa sa zoznam: prvkami sú susedné body (dvojica bodov)
- náhodne sa vyberie prvok zo zoznamu (dva susedné body)
- v
1/3a2/3dĺžky medzi nimi vytvor a vykresli body(C,D) - vypočítaj a vykresli bod
E, aby vznikol rovnostranný trojuholníkCDE - pridaj do zoznamu dvojice bodov
(AC),(CE),(ED),(DB) - odober zo zoznamu aktuálnu dvojicu (v tomto prípade
AB) - choď na
1.krok

Barnsleyovo papradie
Hodnoty parametrov sú uvedené v nasledujúcej tabuľke. Stĺpce "sada x" v tejto tabuľke predstavujú príslušné transformácie. Parameter p znamená pravdepodobnosť s akou sa vyberie príslušná transformácia.
| ----- | sada 1 | sada 2 | sada 3 | sada 4 |
|---|---|---|---|---|
| a | 0.0 | 0.85 | 0.2 | -0.15 |
| b | 0.0 | 0.04 | -0.26 | 0.28 |
| c | 0.16 | 0.0 | 0.0 | 0.0 |
| d | 0.0 | -0.04 | 0.23 | 0.26 |
| e | 0.0 | 0.85 | 0.22 | 0.24 |
| f | 0.0 | 1.6 | 1.6 | 0.44 |
| p | 0.01 | 0.85 | 0.07 | 0.07 |

Použitím tohto mechanizmu (iteračným spôsobom) sa fraktál s pribúdajúcimi bodmi zostruje , až nakoniec je evidentne rozpoznateľná symetria listu papradia.
Pentigree
Hodnoty parametrov tohto fraktálu sú uvedené v nasledujúcej tabuľke.
| ----- | sada 1 | sada 2 | sada 3 | sada 4 | sada 5 | sada 6 |
|---|---|---|---|---|---|---|
| a | 0.309 | -0.118 | 0.309 | -0.118 | 0.309 | 0.309 |
| b | -0.225 | -0.363 | 0.225 | 0.363 | 0.225 | -0.225 |
| c | 0.0 | 0.309 | 0.191 | 0.5 | 0.382 | 0.691 |
| d | 0.225 | 0.363 | -0.225 | -0.363 | -0.225 | 0.225 |
| e | 0.309 | -0.118 | 0.309 | -0.118 | 0.309 | 0.309 |
| f | 0.0 | 0.225 | 0.588 | 0.363 | 0.0 | -0.225 |
| p | 0.166 | 0.166 | 0.166 | 0.166 | 0.166 | 0.166 |
V tomto prípade sa používa celkovo 6 transformácií. Pravdepodobnosť ich výberu je rovnaká. Ich použitím vznikne nasledujúci obrazec:

Pentadentrite
Hodnoty parametrov tohto fraktálu sú uvedené v nasledujúcej tabuľke.
| ----- | sada 1 | sada 2 | sada 3 | sada 4 | sada 5 | sada 6 |
|---|---|---|---|---|---|---|
| a | 0.341 | -0.038 | 0.341 | -0.234 | 0.173 | 0.341 |
| b | -0.071 | -0.346 | -0.071 | 0.258 | 0.302 | -0.071 |
| c | 0.0 | 0.341 | 0.379 | 0.720 | 0.486 | 0.659 |
| d | 0.071 | 0.346 | 0.071 | -0.258 | -0.302 | 0.071 |
| e | 0.341 | 0.038 | 0.341 | -0.234 | 0.173 | 0.341 |
| f | 0.0 | 0.071 | 0.418 | 0.489 | 0.231 | -0.071 |
| p | 0.166 | 0.166 | 0.166 | 0.166 | 0.166 | 0.166 |
V tomto prípade sa používa celkovo 6 transformácií. Pravdepodobnosť ich výberu je rovnaká. Ich použitím vznikne nasledujúci obrazec:

Levy-ho drak
Hodnoty parametrov tohto fraktálu sú uvedené v nasledujúcej tabuľke.
| ----- | sada 1 | sada 2 |
|---|---|---|
| a | 0.5 | 0.5 |
| b | -0.5 | 0.5 |
| c | 0 | 0.5 |
| d | 0.5 | -0.5 |
| e | -0.5 | 0.5 |
| f | 0 | 0.5 |
| p | 0.5 | 0.5 |
V tomto prípade sa používajú celkovo dve transformácie. Pravdepodobnosť ich výberu je rovnaká. Ich použitím vznikne nasledujúci obrazec:

