Prírodou inšpirované algoritmy

Schéma teoréma

Pre matematický popis a analýzu genetických algoritmov je kľúčovým pojmom pojem tzv. schémy. Pojem schéma slúži na vyjadrenie podobnosti niekoľkých reťazcov, obsahujúcich ten istý stavebný blok (resp. skupinu blokov) reprezentujúci nejakú spoločnú "dobrú" vlastnosť, resp. niekoľko takých vlastností. Každý reťazec, obsahujúci takýto blok je inštanciou tejto schémy bez ohľadu na to, aké číslice obsahuje zbytok reťazca. Inštanciami schémy 101**** (metaznak hviezdička znamená "nezáleží na") sú reťazce 1011111 1010000 1010101 ale nie reťazce 0101111 1110000. Schéma nemusí byť súvislá, teda aj 1**0** a 10**01 sú tiež schémy. Rád schémy o(H) je počet fixovaných ("nehviezdičkových") pozícií a dĺžka schémy d(H) je vzdialenosť medzi prvou a poslednou fixovanou pozíciou schémy H, napr. schéma *1**0* má rád 2 a dĺžku 3.

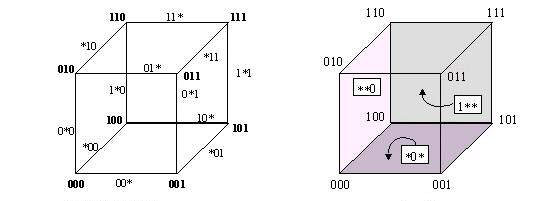Priestor prehľadávania pre binárne reťazce dĺžky 3	Príklad troch schém

Stavebný blok je malá, tesne spriahnutá skupina génov, ktorá reprezentuje nejakú "dobrú" vlastnosť (prejavujúcu sa výrazným príspevkom k vysokej hodnote vhodnosti). Vďaka tomu sa v ďalších generáciách postupne zvyšuje počet jedincov v populácii, ktorí obsahujú tento blok. Hypotéza stavebných blokov (Goldberg, 1989) tvrdí, že GA nájde riešenie tak, že najprv "objaví" čo najviac úspešných stavebných blokov a potom ich kombinuje pomocou kríženia tak dlho, kým sa nájde jedinec s najvyššou vhodnosťou.

Holland odvodil pre prípad reprezentácie binárnymi reťazcami a už skôr spomínaných mechanizmov kríženia a mutácie nasledujúci vzťah pre počet inštancií danej schémy S v generácii t:

m(S,t+1)>=m(S,t)*a*f(S)/f

kde:

m(S,t) je počet inštancií schémy S v generácii t,

m(S,t+1) je očakávaný počet inštancií schémy S v generácii t+1,

f(S) je priemerné ohodnotenie inštancií schémy S v generácii t,

f je priemerné ohodnotenie všetkých reťazcov generácie t,

a<1 je faktor zastupujúci vplyv kríženia a mutácie, jeho podrobnejšie určenie je na obrkázku

Z tohto vzťahu môžeme spraviť základný záver, že počet inštancií krátkej kompaktnej schémy (neovplyvnenej genetickými operátormi), ktorá má nadpriemerné ohodnotenie, s časom rastie, a to približne exponenciálne rýchle, zatiaľ čo počet inštancií schémy podpriemerného ohodnotenia približne exponenciálne klesá.