Prírodou inšpirované algoritmy
študijné materiály pre projekt mobilnej triedy umelej inteligencie
Genetické operátory
Aplikáciou genetických operátorov na rodičov vznikajú ich potomkovia. Pričom tieto operátory umožňujú vznik nových štruktúr v potomkoch. Je možné používať ich voľne a nadefinovať si ľubovoľný vlastný operátor. Konečných potomkov získavame buď sériovou postupnosťou operátorov, alebo ich paralelnou aplikáciou, resp. vzájomnou kombináciou týchto prístupov v pravdepodobnostnom zmysle (t.j. operátor je skutočne použitý len s určitou pravdepodobnosťou danou ako parameter GA).
Genetické operátory možno rozdeliť do 3 skupín
- asexuálne
- sexuálne
- panmiktické
aplikujú sa na jedného rodiča, pričom k nemu pridávajú novú genetickú informáciu.
aplikujú sa na dvoch rodičov, pričom vhodne premiešajú ich genetický materiál.
aplikujú sa na viac ako dvoch rodičov a takisto len vhodne premiešavajú genetický materiál rodičov.
Najčastejším sexuálnym operátorom je kríženie. Za účelom kríženia je najprv nutné vybrané jedince spárovať. Na každý pár je potom aplikované kríženie s nejakou dopredu stanovenou pravdepodobnosťou (obvykle veľmi vysokou, napr. 0,95). Kríženie samo o sebe znamená výmenu genetického materiálu, teda častí reťazcov medzi oboma jedincami. V jednoduchšom prípade môže ísť napr. o to, že sa náhodne určí pozícia a od tejto pozície si oba reťazce vymenia konce
- (jednobodové kríženie zobrazené na nasledujúcom obrázku v ľavo).
- uniformné kríženie vygeneruje sa maska (náhodný binárny reťazec rovnakej dĺžky ako sú chromozómy rodičov) a do potomka sa vyberú tie bity z chromozómu prvého rodiča, na pozícii ktorých je v maske jednička, ostatné bity sa berú z druhého rodiča
- modifikačné kríženie - generuje jediného potomka, ktorý je výsledkom nejakej binárnej operácie nad chromozómami rodičov.
Existuje mnoho rôznych typov krížení, vždy je však potrebné voliť taký mechanizmus, aby krížením vznikol opäť reťazec, ktorý reprezentuje nejaké prípustné riešenie.

jednobodové a trojbodové kríženie

Uniformné a modifikačné kríženie
- V (Kubalík a Lažanský, 2000) je opísaná modifikácia klasického jednobodového, dvojbodového a uniformného kríženia, tzv. PRX operátor (partially randomised crossover operator). Pracuje v dvoch krokoch: najprv sa klasickým postupom vygenerujú dva chromozómy obsahujúce schému, spoločnú obom rodičom. Potom sa v jednom z potomkov invertujú bity náhodne vybranej časti tejto spoločnej schémy. Uvedený postup umožní zabrániť uviaznutiu GA v lokálnom optime.
Mutácia je príkladom asexuálneho operátora, slúži na udržovanie genetickej variácie v populácii a tým bráni, aby proces hľadania skĺzol len do oblasti nejakého lokálneho optima. U binárnych reťazcov sa môže jednať napr. o prehodenie 0 za 1 na nejakej náhodne vybratej pozícii. Pretože však významne narúša genetickú informáciu, malo by byť uplatňovanie obmedzené nejakou pomerne malou pravdepodobnosťou (vo väčšine aplikácií sa táto pravdepodobnosť pohybuje medzi 0,001 a 0,1). Aj tu, podobne ako u kríženia, je potrebné dbať o to, aby mutáciou narušený reťazec opäť reprezentoval nejaké prípustné riešenie.
Príklad GA - nájdenie minima jednorozmernej funkcie
Nasledujúci príklad je inšpirovaný Java appletom, ktorý možno nájsť na stránke http://cs.felk.cvut.cz/~xobitko/ga/. Ide o GA na nájdenie minima jednorozmernej funkcie definujúcej priestor prehľadávania zobrazený na nasledujúcom obrázku
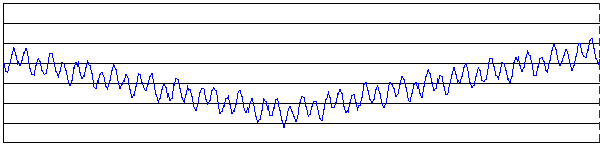
Prehľadávaný priestor
Na vodorovnej osi grafu sú lineárne zoradené body priestoru - možné riešenia. Ich funkčná hodnota určujúca vhodnosť predstavuje zvislú súradnicu. Hľadaný extrém funkcie zobrazenej modrou čiarou je označený ako min.
Každá populácia pozostáva z binárnych chromozómov dĺžky 32, ich dekadická hodnota určuje polohu bodu priestoru prehľadávanie na vodorovnej osi, kde 0 sa nachádza vľavo a vpravo je hodnota 4294967295 (2^32 -1)(modrý štvorček predstavuje 0 a sivý 1).Začína sa s náhodne inicializovanou populáciou jedincov, ktorá je usporiadaná podľa vhodnosti.
Pre lepšie pochopenie činnosti genetických algoritmov poslúži popis procesu formovania novej generácie zobrazený na obrázkoch. Z aktuálnej populácie sú najprv do novej populácie skopírované dva najlepšie jedince elitizmus. Potom sa postupne dopĺňajú zvyšné jedince, až kým nie je nová populácia kompletná. Nová populácia je tvorená potomkami rodičov, ktorí sú vybraní selekciou, následne je na nich aplikované kríženie s určitou pravdepodobnosťou. Krížením vznikajúci potomkovia sú potom mutovaní s nejakou pravdepodobnosťou a vložení do novej populácie. V ďalšom kroku algoritmu táto populácia nahradí predchádzajúcu, pričom je opäť usporiadaná podľa vhodnosti. Takto algoritmus postupuje cez generácie.
 |  | |
Aktuálna generácia | Nová generácia |
Jedince 0 a 1 sú aplikovaním elitizmu skopírované z aktuálnej populácie.
Umiestnenie jedincov týchto populácii v priestore prehľadávania vyzerá nasledovne:
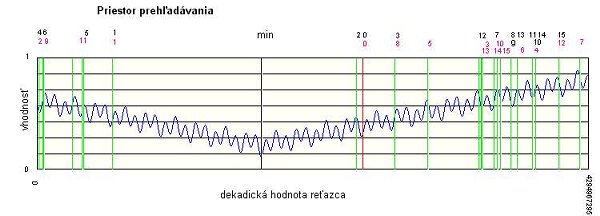
Priestor prehľadávania
Selekciou boli za rodičov vybraní jedinci:
- jedinec 0 ...... 1-krát
- jedinec 1 ...... 1-krát
- jedinec 3 ...... 2-krát
- jedinec 4 ...... 1-krát
- jedinec 5 ...... 1-krát
- jedinec 7 ...... 2-krát
- jedinec 9 ...... 1-krát
- jedinec 12 ...... 1-krát
- jedinec 13 ...... 3-krát
- jedinec 15 ...... 1-krát
Na nasledujúcom obrázku je postupný vznik jedincov 2 a 3.
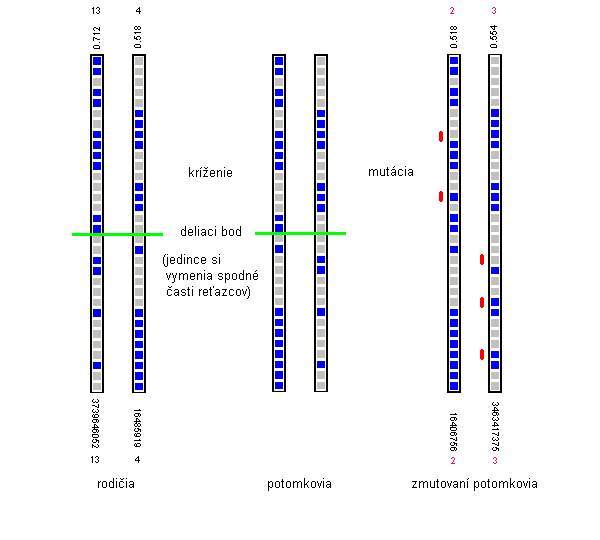
Príklad kríženia a mutácie
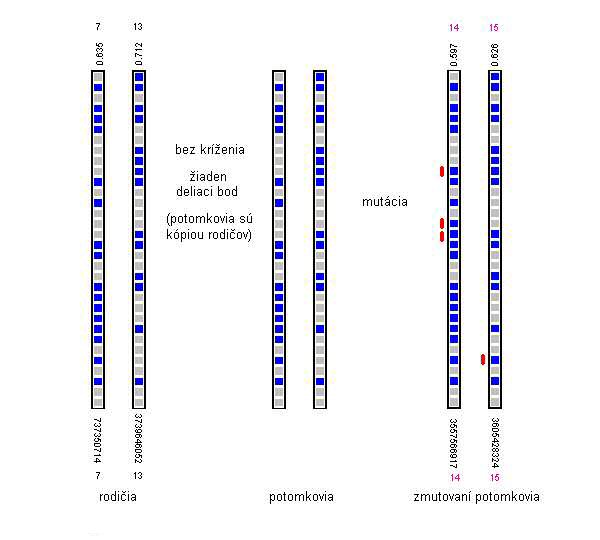
Na obrázku pod textom je postupný vznik jedincov 14 a 15, kde možno vidieť, že nie vždy musí dôjsť ku kríženiu, čo je dané jeho pravdepodobnosťou aplikácie. (to isté platí aj pre mutáciu).