Prírodou inšpirované algoritmy

Reverzibilné Celulárne Automaty

Ako hovorí predchádzajúca kapitola Fyzika a Reverzibilný Celulárny Automat - RCA, reverzibilný celulárny automat spĺňa vlastnosti:

• lokálnosť- deje sa odohrávajú lokálne. Stav bunky závisí iba od predchádzajúcich stavov okolitých buniek
• reverzibilita - kde platí, že informácia sa nemôže vytrácať ani vznikať, môže iba zmeniť svoju formu.

Známa Conwayova hra života, ktorá je založená na jednoduchých pravidlách susedstva nie je reverzibilný CA. Napriek tomu, že počet všetkých možných stavov do ktorých sa môže CA dostať je K.K!, pri väčšine počiatočných konfigurácií sa CA dostane do oscilácií po veľmi krátkom čase. To spôsobuje to, že takýto CA dáva k dispozícii len malý čas na to aby v ňom vznikla nejaká komplexná forma či bohaté usporiadanie - evolúcia.

Ako hovorí (Margolus, 1998) reverzibilné automaty nie sú charakteristické takýmto správaním. Nevieme povedať ako dlho bude cyklus trvať. Je to spôsobené tým, že reverzibilné dynamické systémy majú dlhé cykly. V prípade reverzibilného systému nemôže dôjsť k tomu aby sa zopakoval stav, ktorý už v systéme nastal pokiaľ sa nezopakuje stav v ktorom systém začal. Inými slovami povedané v každom stave, okrem počiatočného, vieme povedať v akom stave sa systém nachádzal predtým. Vzhľadom na to, že v takomto systému v podstate nie je nič čo by systém tlačilo do počiatočného stavu je teda veľmi pravdepodobné, že predtým ako sa systém doň opätovne vráti prejde množstvom stavov. Ak by systém menil svoje stavy skutočne náhodne tak by systém štatisticky musel prejsť cez polovicu všetkých možných stavov, ktoré môžu nastať kým by sa systém vrátil do pôvodného stavu.
Preto pri snahe pozorovať systém, ktorý bude dostatočne dlho trvať a vytvárať zaujímavé konfigurácie je vhodné aby bol reverzibilný.

Vybrané druhy Reverzibilných Automatov - RCA

Všetky druhy tu spomínaných reverzibilných automatov vychádzajú z CA (z anglického Cellular Automata - celulárny automat), ktorý navrhol Margolus. V jeho CA je bunka ohraničená striedaním plnej a bodkovanej čiary tak ako to vyobrazuje nasledujúci obrázok. Jednotlivé lokálne pravidlá sú potom aplikované na blok štyroch buniek ohraničených striedavo raz plnými a potom bodkovanými čiarami. Ak v takomto systéme počet buniek v stave A pre danú štvoricu buniek ostáva nemenný potom sa taktiež nemení celkový počet buniek v stave A aj v globálnom merítku - na celej mriežke. Tým sa zabezpečí zachovanie informácií. Naviac ak je úprava pre každú takúto štvoricu reverzibilná potom je reverzibilný aj celý CA .

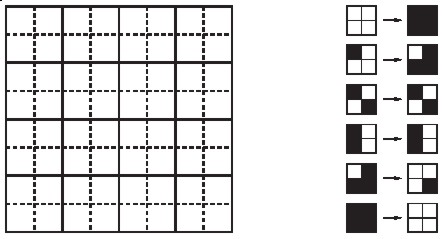
Prvým takýmto príkladom reverzibilného CA je Critters. Je to CA, ktorý sa vyvíja do zaujímavej zložitosti. Lokálne pravidlá, ktoré popisuje nasledujúci obrázok používajú blok 2x2 buniek na dvojrozmernej mriežke. Samozrejme nie sú zobrazené všetky možné kombinácie stavov jednotlivých polí nakoľko zvyšné konfigurácie môžeme dostať jednoduchým rotovaním týchto o 90 stupňov. Každý stav má svoj jednoznačný obraz a teda ide o bijektívne zobrazenie čo zabezpečuje reverzibilnosť tohoto automatu.

Nie je veľmi zaujímavé spustiť tento CA z úplne náhodného stavu ako by to mohlo byť v prípade už spomínanej hry života. Je to preto, že väčšina stavov vyzerá viac-menej náhodne. Nasledujúci obrázok zobrazuje počiatočný stav, stav po milión krokoch a detail oblasti tohto stavu z pravej strany.

Podobne ako pri hre života aj v Critters existujú malé pohybujúce sa objekty nazývané klzáky. Ak dva klzáky prídu do kolízie vytvoria maličký zhluk ôsmych buniek, ktorý sa potupne mení. Ak po dlhšom čase nič nekoliduje so zhlukom vznikne jeden alebo dva klzáky. Táto vlastnosť je zapríčinená vlastnosťami zachovania a reverzibility. Zo zákona reverzibility sa dá dokázať, že zhluk sa musí po čase rozpadnúť a naviac keďže jediné pohybujúce sa objekty, ktoré môžu vzniknúť z ôsmych buniek sú jeden alebo dva klzáky je jasné, že je to jediná vec ktorá z takéhoto zhluku môže vzniknúť.

Ďalším príkladom je Biliardový model celulárneho automatu (z anglického: Billiard Ball Model CA - BBMCA). Stránka BBM, ktorá je súčasťou tohoto tutorialu detailne popisuje tento model a preto sa týmto modelom nebudeme viac zaoberať.

Pri konštrukcií rôznych druhov CA sa ukazuje, že niektoré z nich by mohli celkom dobre popisovať molekulárnu dynamiku či už v plyne alebo v kvapaline. Príkladom môže byť CA ktorý vychádza z lokálnych pravidiel BBMCA a modeluje štvorsmerový plyn na dvojrozmernej mriežke. Nasledujúci obrázok zobrazuje lokálne pravidla, ktoré sú bijektívne podobne ako v predchádzajúcich prípadoch. Náhodne vyplnený priestor predstavuje strednú koncentráciu plynných častíc a čierny štvorček uprostred predstavuje vysokú koncentráciu plynu. Posledný obrázok znázorňuje plyn po 200 krokoch.

Je to postupujúca tlaková vlna, ktorá sa pohybuje od stredu k okraju. Na tomto CA je zaujímavé to, že takéto správanie sa dosiahlo veľmi jednoduchými lokálnymi pravidlami, čo motivovalo mnohých k hlbšiemu štúdiu týchto druhov celulárnych automatov (Margolus, 1998).