Prírodou inšpirované algoritmy

Kruh buniek - matematický popis a riešenie

Kruh buniek

Z veľkého počtu geometrických útvarov, v ktorom môžu byť bunky zoskupené, patrí kruhové zoskupenie k tým najjednoduchším, a môžeme na ňom ľahko ukázať vytvorenie diferenciálnych rovníc.

Predpokladajme, že máme N rovnakých buniek a dva podstatné morfogény X a Y. Nepodstatných morfogénov môže byť aj viac. Napr. takých, ktoré slúžia ako katalyzátor v reakcii medzi podstatnými morfogénmi. Koncentráciu X v bunke r označíme ako Xr a koncentráciu Y v r ako Yr. V každej bunke r, kde 1 ≤ r ≤ N dochádza k difúzii s bunkami r-1 a r+1. Medzibunková difúzna konštanta pre X je µ a pre Y je ν. Na jednotku rozdielu koncentrácie látky X dochádza k difúzii bunky so susednou bunkou, ktorá ma menšiu koncentráciu, v pomere µ. Podobne je to s morfogénom Y a konštantou ν. Taktiež musíme brať do úvahy intenzitu chemickej reakcie. Predpokladajme, že chemická reakcia má tendenciu zvyšovať morfogén X v pomere f(X,Y) a morfogén Y v pomere g(X,Y). Ak sa zoberú do úvahy aj zmeny X a Y spôsobené difúziou, správanie systému popíšeme 2N diferenciálnymi rovnicami.

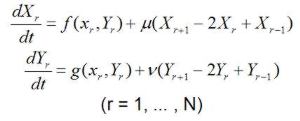
Ak f(h,k):g(h,k)=0, potom izolovaná bunka je v rovnovážnom stave pri koncentrácii X=h, Y=k. Rovnovážny stav v tomto kruhovom systéme sa dosiahne ak Xr=h a Yr=k. Môže to byť stabilný alebo nestabilný rovnovážny stav. Ak predpokladáme, že systém je blízko rovnovážneho stavu môžeme napísať: Xr=h+xr, Yr=k+yr. To isté môžeme vyjadriť aj rovnicami: ax+by pre f(h+x, y+k) a cx+dy pre g(h+x, y+k). Keďže f(h,k)=g(h,k)=0 nie potrebné definovať už žiadnu konštantu. Predpokladáme, že x a y sú malé čísla, a preto členy s vyššími mocninami x a y môžeme zanedbať. Hodnoty a, b, c, d predstavujú hraničné reakčné intenzity. Všeobecne môžu byť popísané maticou s počtom prvkov M2, kde M predstavuje počet morfogénov. Hraničná reakčná intenzita má rozmery recipročnej hodnoty za čas. Ako jej príklad môžeme uviesť napr. intenzitu rádioaktívneho rozpadu.

Za týchto predpokladov môžeme rovnice zapísať nasledovne:

Na vyriešenie týchto rovníc zavedieme nové súradnice

.

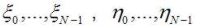A potom:

.

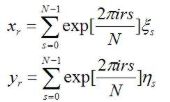To sa dá zapísať aj ako

.

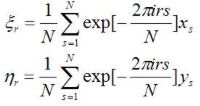Za použitia vzorca

.

dostaneme

.

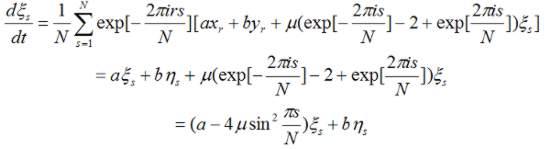a obdobne

.

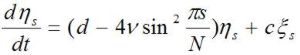Dostali sme rovnice so separovateľnými premennými. Dve rovnice prislúchajú ξ1 a η1, dve ξ2 a η2 atď. Tieto rovnice sú lineárne s konštantnými koeficientmi. Nech ps a ps´ sú korene rovnice.

.

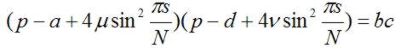Potom riešenie rovníc je

.

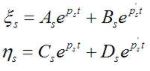Kde koeficienty As, Bs, Cs, Ds nie sú nezávislé, ale sú obmedzené a spĺňajú

.

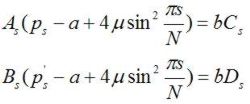Ak p_s=p_s', rovnice sa zmenia na

.

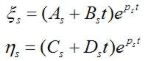Spätnou substitúciou a nahradením premenných xr, yr premennými Xr, Yr (aktuálne koncentrácie) dostávame riešenie

.

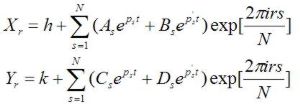kde As, Bs, Cs, Ds sú ľubovolné komplexné čísla.