Prírodou inšpirované algoritmy

Fredkinove hradlo

Fredkinove hradlo

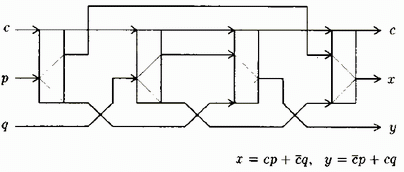
Fredkinove hradlo je základný element v teórii zachovávania logiky (conservative logic) vyvinutý Edwardom Fredkinom a Tomasom Toffolim. Toto hradlo je reverzibilné, pretože logická funkcia je injektívna. Okrem toho je to ešte bit zachovávajúce hradlo, pretože medzi vstupom a výstupom sa zachováva počet jednotiek. Fredkinove hradlo je zobrazené na nasledujúcom obrázku.

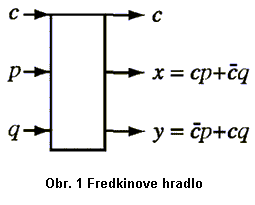
Fredkinovým hradlom je kombinačný logický element, ktorým je možné realizovať logické funkcie ako sú AND, OR, NOT a vetvenie. Z toho potom vyplýva, že každý sekvenčný obvod môže byť realizovaný Fredkinovým hradlom s nejakým časovým oneskorením.

Fredkinove hradlo je základnou časťou biliardového automatu (BBM). BBM je fyzikálny výpočtový model, ktorého logické operácie sú realizované elastickými zrážkami ideálnych gúľ ( navzájom si odovzdajú energiu a to bez straty energie v okolí).

Na realizáciu Fredkinovho hradla v BBM sú použité jednoduchšie logické hradlá, ktoré sa nazývajú interakčné hradlo a prepínacie hradlo.

Interakčné hradlo

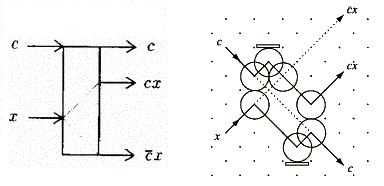
Interakčné hradlo (I-hradlo) má 2 vstupy a 4 výstupy (nasledujúci obrázok). Je reverzibilné a bit zachovávajúce hradlo. Priamo realizuje zrážky dvoch gúľ v biliardovom modeli (BBM).

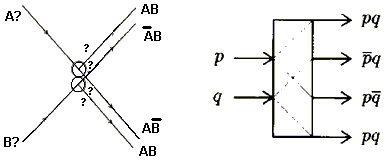
Na nasledujúcom obrázku je inverzné interakčné hradlo, ktoré má naopak 4 vstupy a 2 výstupy. Vykonáva inverzné logické funkcie ako I-hradlo.

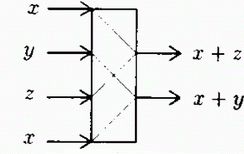
V inverznom I-hradle prvý a posledný zo štyroch vstupov musí musia mať rovnakú hodnotu x a x,y,z musia mať vzájomne vylučujúce sa hodnoty (t.j. najviac jeden z nich môže nadobúdať hodnotu logická 1), aby si zachoval reverzibilitu.

Prepínacie hradlo

Prepínacie hradlo (S-hradlo) má 2 vstupy a 3 výstupy, je reverzibilné a bit zachovávajúce hradlo. Na nasledujúcom obrázku je zobrazené v ľavej časti S-hradlo, spolu aj s modelom.

Inverzné prepínacie hradlo realizuje inverznú funkciu S-hradla za predpokladu, že vstupy vyhovujú podmienkam:

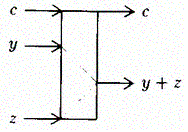
Na nasledujúcom obrázku je ukázané ako je F-hradlo zostrojené pomocou dvoch S-hradiel a dvoch inverzných S-hradiel.