Prírodou inšpirované algoritmy

Plánovanie

Pod plánovaním rozumieme vytváranie plánu ako pomocou informácií o stave rôznych objektov prostredia (prichádzajúcich z vonkajších receptorov) a informácií o vnútornom stave systému vygenerovať patričnú odozvu efektorov, ktorá spôsobí žiadanú zmenu stavu prostredia.

Simulácia správania sa "mravca Santa Fe "

Typickou ukážkou plánovacej úlohy je navigácia umelého mravca tak, aby pozbieral všetku potravu rozmiestnenú v prostredí na nepravidelnej neúplnej dráhe tzv. Santa Fe trail. Umelý mravec sa pohybuje v toroidálnej mriežke rozmerov 32*32, v ktorej je umiestnených 89 kúskov potravy. Je vybavený jediným senzorom schopným rozoznať prítomnosť potravy na políčku priamo pred mravcom. Vykonávať môže jednu z troch základných akcií:

1. Right otočenie doprava o 90 stupňov
2. Left otočenie doľava o 90 stupňov
3. Move pohyb vpred, v prípade, že sa na políčku pred ním nachádzala potrava ju mravec vezme

Realizácia

Pri realizácii tejto úlohy bol opäť použitý postup navrhnutý J. R. Kozom.

• Množina terminálov pozostávala z troch základných akcií : T={Move, Right, Left}
• Množina primitívnych funkcií pozostávala z troch funkcií : F={IF-FOOD-AHEAD, PROGN2}

1. IF-FOOD-AHEAD, je funkcia s dvoma argumentami a jedným vstupným parametrom, vstupom senzoru mravca. Funkcia vykoná (evalvuje zmysle v Lisp-ovského vykonania) prvý argument v prípade, že sa pred mravcom nachádza jedlo, inak vykoná druhý argument.
2. PROGN2, funkcia sekvenčne vykoná oba zo svojich dvoch argumentov.
3. PROGN3, trojargumentový ekvivalent funkcie PROGN2.

Ohodnotenie jedinca bolo vykonávané nasledovne : Mravec reprezentujúci ohodnocovaného jedinca bol umiestnený do arény na pozíciu so súradnicami [1,1] otočený smerom nahor (viď obrázok nižšie), kde zbieral potravu po dobu 400 vnútorných cyklov.
Po ich skončení je jedincovi priradená:

• raw fitness = počet pozbieraných kúskov potravy
• stand. fitness = počet nepozbieraných kúskov potravy
• adjust. fitness = 1 / (1 + stand. fitness)

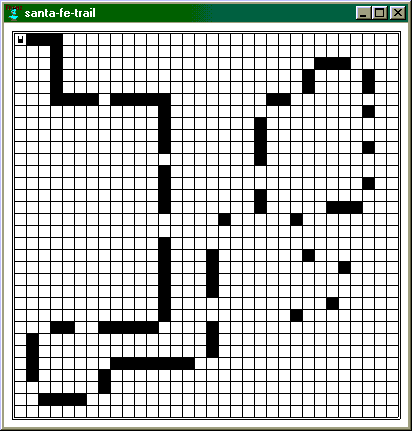
Mravcov svet

Parametre evolučného procesu :

• Veľkosť populácie M =5 00
• Maximálny počet generácií G = 51 (generácie 0 až 50)
• Pravdepodobnosť kríženia Pc = 0.9
• Pravdepodobnosť reprodukcie Pr = 0.1
• Pri výbere bodu prekríženia pri krížení pravdepodobnosť výberu vnútorného bodu 90% a pravdepodobnosť výberu vonkajšieho bodu 10%
• Maximálna hĺbka vytváraných jedincov Dcreated = 17
• Maximálna hĺbka iniciovaných jedincov Dinitial = 6
• Použitá 90% decimácia (na rozdiel od experimentov popísaných J. Kozom)
• Mutácia, permutácia a editácia nepoužité

Evolučný proces bol ukončený po prebehnutí 51 generácií, alebo v prípade nájdenia jedinca schopného pozbierať počas 400 krokov všetku potravu. V 27 generácii bolo nájdené riešenie tvaru:

   (IF-FOOD-AHEAD
        (MOVE)
        (PROGN2
	     (LEFT)
	     (IF-FOOD-AHEAD
                  (MOVE)
		  (PROGN3
		        (RIGHT)
			(RIGHT)
	                (IF-FOOD-AHEAD
		             (MOVE)
		             (PROGN2
		                  (LEFT)
			          (MOVE))))))) 

Mravec používajúci túto stratégiu bol schopný pozbierať počas 400 cyklov 88 z 89-ich kúskov potravy. Jeho stratégia je v podstate jednoduchá :
Najprv zistí, či sa jedlo nachádza na políčku priamo pred ním. Ak áno, prejde na toto políčko a vezme potravu, ktorá na ňom leží. Ak nie, otočí sa vľavo a opäť skontroluje, či sa pred ním nachádza jedlo. Ak ho nenájde ani tam, otočí sa dvakrát doprava a tam hľadá potravu. Ak ju nenájde, otočí sa späť aby získal pôvodnú orientáciu a pohne sa dopredu.

Táto stratégia umožňuje mravcovi prejsť celú dráhu a nájsť všetku potravu. Posledný kúsok potravy mravec nevzal len kvôli nedostatku času, v prípade, že by mal k dispozícii ešte zopár cyklov bol by dosiahol kompletné riešenie úlohy.

Zdrojové súbory s lisp-ovskými programami riešiacimi túto úlohu.