Prírodou inšpirované algoritmy

Algoritmus tvorby MM aJM

Algoritmus tvorby MM:

1. z0 = 0; i = 1,
2. Zoberiem si bod z komplexnej roviny a označím si ho ako c (pozor bod c je komplexné číslo),
3. Vypočítam si z1 = z02 + c = 02 + c = c. Takže v prvom kroku sa z1 rovnalo priamo bodu z komplexnej roviny,
4. Vypočítame si zi+1 = zi2 + c. Keďže sa jedná o komplexné čísla, táto operácia je veľmi časovo náročná, ale ako poznáme z teórie komplexných čísel dá sa to vypočítať osobitne pre reálnu a osobitne pre imaginárnu časť, a to nasledovným spôsobom :
   • z(i+1)re=zi re2 - zi im2 + cre
   • z(i+1)im=2 * zi re * zi im + cim,
5. Zistíme si, či modul z(i+1) nepresiahol hodnotu 2 (čiže či nediverguje) a to nasledovným spôsobom: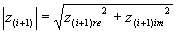

   

6. Ak |z(i+1)| < 2 a zároveň i<=N, kde N je nami zvolené číslo potom i=i+1 a pokračujeme v kroku 4. inak krok 7.
7. Ak i <= N (nami zadané číslo), potom zafarbi bod c na farbu prislúchajúcu danému číslu i inak daný bod patrí do MM a zafarbi ho na čierno.

Tento cyklus sa opakuje pre celú komplexnú rovinu a tým vznikne MM.

Algoritmus tvorby JM:

1. i=1,
2. Zoberiem si bod z komplexnej roviny a označím si ho ako c (pozor bod c je komplexné číslo),
3. Vypočítame si zi+1=zi2+c. Keďže sa jedná o komplexné čísla, táto operácia je veľmi časovo náročná, ale ako poznáme z teórie komplexných čísel dá sa to vypočítať osobitne pre reálnu a osobitne pre imaginárnu časť, a to nasledovným spôsobom:
   • z(i+1)re = zi re - zi im + cre
   • z(i+1)im = 2 * zi re * zi im + cim,
4. Vypočítame si modul z(i+1) a to nasledovným spôsobom: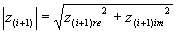

   

5. Ak |zi+1| < 2 a zároveň i<=N, kde N je nami zvolené číslo, potom i=i+1 a pokračujeme v kroku 3 inak krok 6.
6. Ak i <= N (nami zadané číslo), potom zafarbi bod c na farbu prislúchajúcu danému číslu i, inak daný bod patrí do JM a zafarbi ho na čierno.

Tento cyklus sa opakuje pre celú komplexnú rovinu a tým vznikne JM.