Prírodou inšpirované algoritmy

Diskrétna logistická rovnica.

Štandardný tvar logistickej rovnice:

kde parameter r je kladná konštanta a predstavuje reprodukčný parameter. Presné riešenie rovnice je známe len pre hodnoty r = 2 , r = -2 a r = 4.

Prvé tri iterácie vyzerajú nasledovne:

x1 = rx(1-x)

x2 = r2(1-x)x(1-rx+rx2)

x3 = r3(1-x)x(1-rx+rx2) (1-r2x+r2x2+r3x2- 2r3x3+r3x4)

Na obrázku sú grafy prvých päť iterácií logistickej rovnice pre niektoré hodnoty r, pre "všetky" hodnoty x(0) z intervalu (0; 1>.

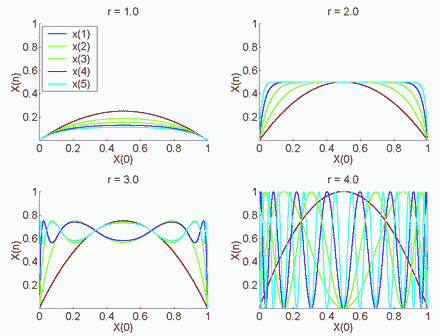
Aby logistická rovnica ako model nestrácala zmysel, všetky hodnoty xn , n = 0,1,2,3,... musia ležať v intervale (0; 1>. Potrebujeme teda určiť interval hodnôt r, pri ktorom táto podmienka je splnená. Maximálnu hodnotu xn+1 ľahko zistíme, ak vypočítame prvú deriváciu dxn+1/dxn logistickej rovnice a dáme rovné nule, teda vypočítame extrém:

Z toho dostaneme, že xn+1 nadobudne svoju maximálnu hodnotu v xn = 1/2. Dosadením tejto hodnoty do logistickej rovnice : xn+1 = max(xn+1) = r / 4. Z tohto vzťahu a z už spomenutej podmienky vyplýva, že r sa musí nachádzať v intervale (0; 4>.

Logistickú rovnicu riešime ako sústavu dvoch rovníc: xn+1 = rxn(1-xn) a xn = xn+1 . Nasledujúci obrázok ukazuje tzv. cobweb diagram (cobweb - pavučina), t.j. grafickú reprezentáciu iteračného procesu.

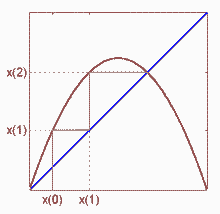
Bod, kde sa krivky pretínajú je riešenie rovnice x = f(x). Ten bod, do ktorého sa postupnou iteráciou dokonvergujeme, sa nazýva stabilné riešenie. Ako na obrázkoch vidno, v tomto prípade na intervale (0; 1> sústava rovníc má dve riešenia. Druhé riešenie je v bode 0, toto riešenie je nestabilné. Riešenie je stabilné, ak platí: |dxn+1/dxn| < 1 , n = 0,1,2,... . Teda, ak absolútna hodnota smernice dotyčnice v bode riešenia je menšia ako smernica diagonály. Na nasledujúcom obrázku je dotyčnica nakreslená zelenou farbou a "absolútna hodnota" dotyčnice svetlomodrou farbou. Pre počiatok súradnicovej sústavy táto podmienka nie je splnená a preto predstavuje nestabilné riešenie.

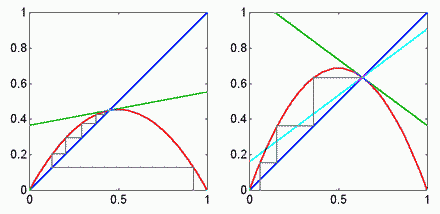
Logistická rovnica má tri režimy chovania: ustálený, periodický a chaotický.