Prírodou inšpirované algoritmy

Citlivosť na počiatočné podmienky.

Majme funkciu f(x) = 4x(1 - x) a počiatočnú podmienku x = x0 . Časový priebeh prvých 20 iterácií ukazuje obrázok.

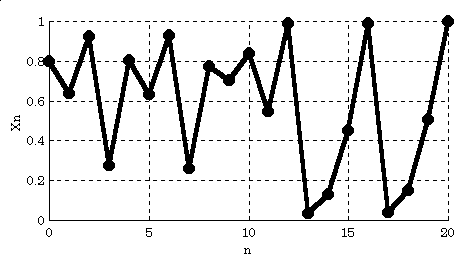
Teraz pripočítajme malú chybu 0.001 k x0, dostávame novú počiatočnú podmienku u = u0 = x0 + 0.001 . Časový priebeh tej istej funkcie pre u0 na obrázku je vykreslený červenou farbou.

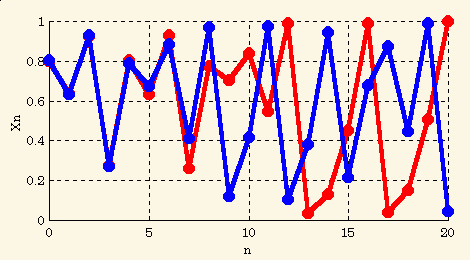
Na ďalšom obrázku vidíme chybu - absolútnu hodnotu rozdielov dvoch priebehov.

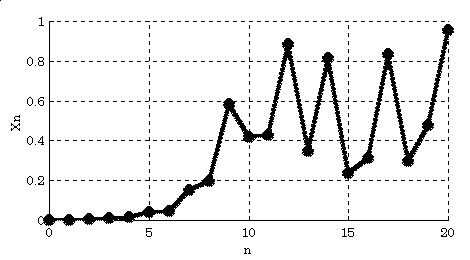
Ako to grafy ukazujú, stavy po prvých iteráciach ostávajú blízko seba, na konci ale chyba narastá do takej miery, že dosiahne veľkosť samotného časového priebehu. Tento jav sa nazýva citlivosť na počiatočné podmienky, jeho populárny názov je motýlí efekt. Citlivosť na počiatočné podmienky je jedným z príznakov chaotického systému. Nie všetky citlivé systémy sú však chaotické.

Príznaky chaotického systému:

• citlivosť na počiatočné podmienky
• výskyt periodických cyklov s periódou 3
• nelinearita

Logistická rovnica spĺňa všetky tri podmienky.

Poznámka: obrázky boli generované v Matlab 5.3 .